Применение условий равновесия тела
1. Виды равновесия. Равновесие тела на опоре
Поставим опыт
Обведем мелом или карандашом основание стоящего на столе цилиндра (рис. 36.1). Фигуру, ограниченную полученной окружностью, будем называть площадью опоры. (В соответствии со сложившейся терминологией площадью опоры называют в данном случае не площадь фигуры, а саму фигуру).
Линия действия силы тяжести пересекает площадь опоры (рис. 36.2).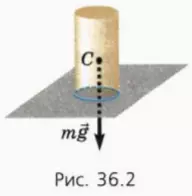
Если наклонить цилиндр на небольшой угол, равновесие нарушится, потому что алгебраическая сумма моментов силы тяжести m и силы нормальной реакции
и силы нормальной реакции  опоры не будет равна нулю (например, относительно центра тяжести) (рис. 36.3).
опоры не будет равна нулю (например, относительно центра тяжести) (рис. 36.3).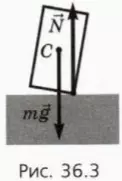
Если отпустить цилиндр, то под действием этих сил цилиндр вернется в начальное положение. Такое положение называют устойчивым равновесием.
? 1. Чему равен тангенс максимального угла, на который можно наклонить стоящий на столе цилиндр радиусом r и высотой h (рис. 36.4), чтобы он вернулся в начальное положение?
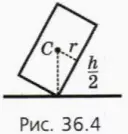
Заметим теперь, что положение, показанное на рисунке 36.4, тоже соответствует равновесию цилиндра!
? 2. Объясните, почему в этом положении оба условия равновесия для цилиндра выполнены.
Однако если отпустить цилиндр, то он не удержится в этом положении: при малейшем отклонении от этого положения действующие на цилиндр сила тяжести и сила нормальной реакции опоры будут отклонять цилиндр еще дальше от положения равновесия. Такое равновесие называют неустойчивым.
? 3. Изобразите схематически куб и конус в положении неустойчивого равновесия на горизонтальной поверхности. Может ли шар находиться в положении неустойчивого равновесия на этой поверхности?
Это задание дает нам пример еще одного вида равновесия (кроме устойчивого и неустойчивого). Шар на горизонтальной поверхности находится в равновесии при любом положении: если перекатить шар в любую другую точку поверхности, он снова окажется в положении равновесия. Такое равновесие называют безразличным.
? 4. Какие из следующих тел могут находиться в безразличном равновесии на горизонтальной поверхности: призма, конус, пирамида, цилиндр? Какие из этих тел могут находиться на горизонтальной поверхности в устойчивом равновесии? Для каких тел существует положение неустойчивого равновесия? Считайте, что проскальзывания нет.
Опыт и расчет показывают, что тело на опоре может находиться в равновесии только при условии, что линия действия силы тяжести пересекает площадь опоры.
Площадью опоры является фигура наименьшего периметра, описанная вокруг всех точек опоры тела. Например, площадь опоры стола на четырех ножках – это прямоугольник, вершины которого – точки соприкосновения ножек стола с полом.
? 5. Крышка стола массой m – квадрат со стороной d. К углам крышки прикреплены легкие ножки высотой H, которые перпендикулярны крышке стола. Стол приподнимают за одну из сторон его крышки. Считайте, что при этом ножки стола не проскальзывают по полу.
а) Насколько надо приподнять центр тяжести стола, чтобы стол после этого опрокинулся?
б) Какую работу при этом надо совершить?
Подсказка. При подъеме центра тяжести тела на h совершается работа mgh.
Цилиндр на наклонной плоскости
Поставим на доску цилиндр высотой h и радиусом r и начнем медленно наклонять доску (рис. 36.5). Коэффициент трения между доской и цилиндром равен μ.
При некотором угле наклона равновесие цилиндра нарушится. При этом возможны два варианта развития событий. Цилиндр может:
1) начать скользить по доске (рис. 36.6);
2) опрокинуться (рис. 36.7).
Чтобы определить, какой из этих двух вариантов реализуется при заданных значениях h, r и μ, можно выбрать такой план действий.
1. Найдем, при каком угле наклона αск цилиндр начнет скользить, если не опрокинется.
2. Найдем, при каком угле наклона αопр цилиндр начнет опрокидываться, если не будет скользить.
3. Из сравнения полученных значений углов αск и αопр сделаем вывод:
– если αопр > αск, то цилиндр начнет скользить, когда угол наклона станет равным αск;
– если αопр ≤ αск, то цилиндр начнет опрокидываться, когда угол наклона станет равным αопр.
При расчетах удобнее сравнивать не углы αск и αопр, а их тангенсы. (Для углов от 0º до 90º неравенства для углов и их тангенсов имеют одинаковый знак.)
? 6. Чему равен тангенс угла наклона αск, при котором цилиндр начал бы скользить, если бы он не опрокидывался?
? 7. Чему равен тангенс угла наклона αопр, при котором цилиндр начал бы опрокидываться, если бы он не скользил?
? 8. На доску ставят цилиндр. Коэффициент трения между доской и цилиндром равен 0,5. Наклон доски медленно увеличивают. При каких из приведенных значений высоты и радиуса цилиндра он начнет скользить по доске? а) h = 3 см, r = 2 см; б) h = 3 см, r = 1 см; в) h = 5 см, r = 1 см.
2. Лестница у стены
К гладкой стене приставляют лестницу (рис. 36.8). При каком условии лестница может остаться в покое? Центр тяжести лестницы в ее середине.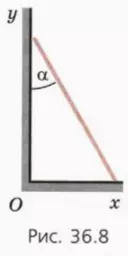
? 9. Почему лестница упадет, если пол гладкий?
Найдя ответ на этот вопрос, вы установите, что прислоненная к стене лестница может покоиться только при условии, что со стороны пола на нее действует сила трения. А поскольку лестница покоится, то это — сила трения покоя.
? 10. Изобразите на чертеже в тетради силы, действующие на лестницу. Введите обозначения:
длина и масса лестницы l и m;
силы нормальной реакции, действующие со стороны стены и пола,  с и
с и  п соответственно;
п соответственно;
сила трения, действующая со стороны пола,  тр;
тр;
коэффициент трения между лестницей и полом μ.
? 11. Объясните, почему справедливы следующие соотношения (α – угол, который составляет лестница с вертикалью):

Подсказка. Воспользуйтесь первым и вторым условиями равновесия (второе – относительно нижнего конца лестницы).
? 12. Объясните, почему справедливо следующее условие равновесия лестницы у гладкой стены:
tg α / 2 ≤ μ (5)
? 13. При каком максимальном угле между лестницей и стеной лестница может покоиться, если коэффициент трения между лестницей и полом равен 0,5?
Выполнение неравенства (5) гарантирует, что лестница без нагрузки может покоиться. А можно ли по этой лестнице взобраться до самого верха?
? 14. Грузный человек взбирается по легкой лестнице. Какое соотношение между α и μ должно выполняться, чтобы человек мог подняться до самого верха лестницы? Считайте, что массой лестницы можно пренебречь по сравнению с массой человека.
Выполнив это задание, вы обнаружите, что для безопасного подъема по очень легкой лестнице угол между лестницей и стеной должен быть существенно меньше, чем для равновесия лестницы без нагрузки.
Палочка в стакане
Пусть в гладком цилиндрическом стакане находится гладкая тонкая палочка длиной l и массой m. Палочка опирается на край стакана (рис. 36.9).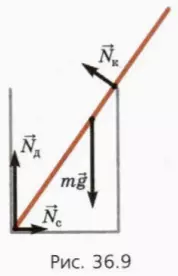
Обозначим высоту стакана h, а его диаметр – d.
Какие силы действуют на палочку?
Прежде всего, это сила тяжести m , приложенная в центре тяжести палочки (он совпадает с ее серединой).
, приложенная в центре тяжести палочки (он совпадает с ее серединой).
Кроме этого, на палочку действуют силы со стороны края стакана, его дна и стенки. Поскольку палочка и стакан гладкие, это – силы нормальной реакции, направленные перпендикулярно поверхности соприкосновения тел. Обозначим эти силы соответственно  к,
к,  д и
д и  с (рис. 36.9).
с (рис. 36.9).
Для упрощения дальнейших формул введем угол α между палочкой и вертикалью, а длину находящейся палочки обозначим b.
? 15. Сделайте в тетради чертеж, на котором обозначены все необходимые величины, и объясните, почему справедливы следующие уравнения:
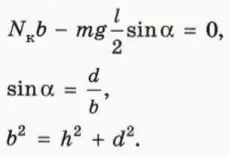
? 16. С какой силой давит палочка длиной 15 см и массой 100 г на край стакана? Высота стакана 8 см, диаметр – 6 см. (Согласно третьему закону Ньютона палочка давит на край стакана с такой же по модулю силой, с какой край стакана давит на палочку.)
Колесо и ступенька
Колесо радиусом r и массой m упирается в ступеньку высотой h (рис. 36.10). Будем считать, что проскальзывания между колесом и ступенькой нет.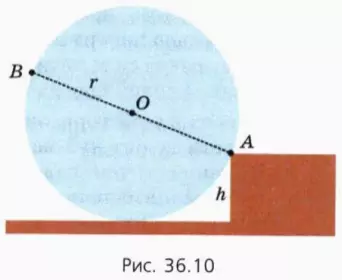
Колесо пытаются вкатить на ступеньку, прикладывая к нему силу в одной точке.
? 17. В какой точке надо приложить к колесу наименьшую силу  , необходимую для того, чтобы вкатить его на ступеньку? Как направить эту силу?
, необходимую для того, чтобы вкатить его на ступеньку? Как направить эту силу?
? 18. Чему равно плечо силы тяжести колеса относительно точки A?
? 19. Чему равна минимальная сила, которую надо приложить к колесу, чтобы вкатить его на ступеньку?
Подсказка. Воспользуйтесь правилом моментов относительно точки A.
Дополнительные вопросы и задания
20. Шар радиусом r лежит в лунке, сделанной в доске (рис. 36.11). Чтобы шар выкатился из лунки, доску надо наклонить к горизонту на угол α. Чему равна глубина лунки h?
Подсказка. Воспользуйтесь условием равновесия тела на опоре.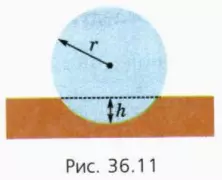
21. Шар массой m и радиусом r закреплен на нити длиной l у гладкой стены (рис. 36.12). Шар находится в равновесии.
а) Объясните, почему продолжение нити проходит через центр шара. Воспользуйтесь правилом моментов относительно центра шара.
б) Чему равна сила натяжения нити?
в) С какой силой шар давит на стену?
22. На шероховатой горизонтальной поверхности лежит куб массой m.
а) В какой точке надо приложить к кубу минимальную силу, чтобы опрокинуть его через его ребро? Считайте, что проскальзывания между кубом и поверхностью нет. Как направить эту силу?
б) Чему равна минимальная сила, которую надо приложить к кубу, чтобы опрокинуть его через ребро?
