🌀 Как рассчитать движение блока массой 5 кг, прикрепленного к стене пружиной жесткостью 500 Н/м

Жесткость пружины — это физическая характеристика, определяющая её способность возвращать форму или размер после того, как она была изогнута, сжата или растянута. Она измеряется в ньютонах на метр (Н/м), что означает силу, необходимую для изменения длины пружины на один метр.

Видео:Два одинаковых бруска толщиной 5 см и массой 1 кг каждый, связанные друг с другом, плавают - №23178Скачать

📐 Формула для расчета силы упругости пружины

Для расчета силы упругости \( F \), которую оказывает пружина, используется формула Гука:

\[ F = k \cdot x \]

где:

• \( F \) — сила упругости, направленная в сторону возврата или расширения пружины, Н (ньютон);
• \( k \) — коэффициент жесткости пружины, Н/м (ньютон на метр);
• \( x \) — удлинение или сжатие пружины относительно начальной точки, м (метр).

Эта формула выражает прямую зависимость между силой упругости, коэффициентом жесткости и удлинением или сжатием пружины. При увеличении удлинения \( x \), сила \( F \), с которой пружина стремится вернуться в исходное положение, также увеличивается пропорционально коэффициенту жесткости \( k \).

Видео:Система из двух грузов, соединенных пружиной жесткости k = 20 н/м движется под действием - №31186Скачать

🔍 Влияние массы блока на движение системы

Масса блока оказывает значительное воздействие на его перемещение. Если масса увеличивается, инерция блока тоже возрастает. Это значит, что требуется большее усилие для начала движения и его остановки.

Понятие инерции связано с массой: чем тяжелее объект, тем сильнее его сопротивление изменениям в движении. В системе с пружиной это означает, что при одной и той же жесткости пружины более тяжелый блок будет двигаться медленнее по сравнению с более легким.

Для понимания сути, представьте, что вы толкаете тележку. Если тележка пустая, её легко сдвинуть с места. Но если она загружена, усилие, необходимое для её движения, значительно возрастает. Точно так же действует и масса блока в нашей системе.

Математически это выражается в уравнении движения, где масса блока участвует как множитель при ускорении. Увеличение массы приводит к снижению ускорения при той же самой приложенной силе.

Когда масса блока увеличивается, изменяется и частота колебаний системы. Чем больше масса, тем медленнее колебания, так как система становится менее чувствительной к изменениям в силе пружины.

Таким образом, масса блока определяет характер движения в системе: от скорости начала движения до частоты колебаний. Чтобы точно определить движение, необходимо учитывать массу как ключевой параметр.

Видео:Урок 39. Простейшие задачи о движении тела, брошенного под углом к горизонтуСкачать

🧮 Как использовать закон Гука для вычислений

Закон Гука описывает, как пружина реагирует на приложенную к ней силу. Он гласит, что сила упругости пропорциональна удлинению или сжатию пружины. Формула выглядит так:

F = -k * x, где:

• F – сила упругости (Н)
• k – жесткость пружины (Н/м)
• x – смещение от равновесного положения (м)

Чтобы использовать закон Гука, необходимо знать жесткость пружины и величину смещения. Например, если жесткость пружины равна 500 Н/м, а смещение составляет 0.1 м, то сила упругости будет равна:

F = -500 * 0.1 = -50 Н

Знак «минус» указывает на направление силы, противоположное смещению. Это значит, что если пружина сжата на 0.1 м, она будет стремиться вернуться в исходное положение, создавая силу в 50 Н.

Закон Гука также позволяет рассчитать смещение пружины под действием известной силы. Для этого можно использовать преобразованную формулу:

x = F / -k

Пример: если к пружине прикладывается сила 100 Н, жесткость которой 500 Н/м, то смещение будет:

x = 100 / -500 = -0.2 м

Таким образом, пружина сожмется на 0.2 м под действием силы 100 Н. Это основные принципы использования закона Гука для вычислений в механике пружин.

Видео:Разбор ЦЭ по физике 2023. Задача Б5 . "Ищем начальную скорость камня"Скачать

📝 Пошаговый пример расчета перемещения блока

Для того чтобы вычислить перемещение блока массой 5 кг, прикрепленного к стене пружиной жесткостью 500 Н/м, необходимо пройти несколько этапов. Рассмотрим их подробно.

Шаг 1: Определяем силу упругости

По закону Гука, сила упругости рассчитывается как произведение жесткости пружины на её удлинение:

F = k * x

Где F — сила упругости, k — жесткость пружины, x — удлинение.

Прикладывая известные значения, получаем:

F = 500 Н/м * x

Шаг 2: Находим ускорение блока

Используя второй закон Ньютона, определяем ускорение блока:

a = F / m

Где a — ускорение, F — сила упругости, m — масса блока.

Подставляем силу упругости и массу блока:

a = (500 Н/м * x) / 5 кг

Шаг 3: Расчет перемещения

Для расчета перемещения воспользуемся формулой кинематики, предполагая начальную скорость равной нулю:

x = 0.5 * a * t^2

Подставляем выражение для ускорения:

x = 0.5 * ((500 Н/м * x) / 5 кг) * t^2

Решая уравнение, находим значение перемещения x в зависимости от времени t.

Таким образом, перемещение блока можно вычислить по этой формуле, учитывая жесткость пружины и массу блока.

Видео:Урок 83. Комбинированные задачи статикиСкачать

🔬 Факторы, влияющие на точность расчетов в реальных условиях

При расчете движения блока, прикрепленного к стене пружиной, множество факторов могут повлиять на точность результатов. Реальные условия редко совпадают с теоретическими допущениями, что приводит к необходимости учитывать различные аспекты. Рассмотрим основные факторы.

1. Трение

Трение между блоком и поверхностью оказывает значительное влияние на точность расчетов. В идеальной ситуации предполагается, что трение отсутствует, однако в реальных условиях оно всегда присутствует. Величина трения зависит от материала блока и поверхности, а также их состояния.

2. Изменение жесткости пружины

В реальной жизни пружина может иметь неоднородную жесткость из-за износа или производственных допусков. Жесткость может изменяться при растяжении или сжатии, что усложняет точные вычисления. Использование качественных и проверенных пружин минимизирует этот фактор, но не исключает его полностью.

3. Температурные изменения

Температура влияет на материал пружины и блока. При изменении температуры материалы могут расширяться или сжиматься, что приводит к изменению характеристик системы. Например, металлические пружины при нагреве могут терять жесткость, что влияет на результаты расчета.

4. Неправильная установка

Неправильная установка блока или пружины, например, под углом или с недостаточной фиксацией, приведет к отклонениям в расчетах. Важно обеспечить правильное крепление всех элементов для получения точных результатов.

5. Аэродинамическое сопротивление

При движении блока через воздух возникает сопротивление, которое замедляет движение и влияет на расчеты. Это особенно важно при высокой скорости или в условиях низкого давления. Влияние аэродинамического сопротивления обычно незначительно, но в некоторых случаях его следует учитывать.

6. Изменение массы блока

Масса блока может изменяться из-за износа, загрязнений или прикрепления дополнительных элементов. Такие изменения приводят к отклонениям в расчетах, так как изменяется сила, действующая на пружину. Регулярная проверка и поддержание массы блока на постоянном уровне помогают минимизировать этот фактор.

Видео:Кубик из пробки с ребром 10 см опускают в воду. Каково отношение объёма кубика - №23044Скачать

📊 Анализ поведения блока при разных значениях жесткости пружины

При изменении жесткости пружины, динамика движения блока значительно варьируется. Параметр жесткости измеряется в Ньютонах на метр (Н/м) и указывает, насколько сильно пружина сопротивляется деформации. Высокая жесткость означает, что пружина будет требовать больше силы для растяжения или сжатия на определенное расстояние.

Сравним движение блока при различных значениях жесткости:

• Малая жесткость (100 Н/м): Пружина слабая, блок перемещается более плавно. Амплитуда колебаний больше, период длиннее.
• Средняя жесткость (500 Н/м): Сила упругости и смещение уравновешены. Блок двигается с умеренной амплитудой и периодом.
• Высокая жесткость (1000 Н/м): Пружина сильно сопротивляется деформации. Блок испытывает быстрые, малые колебания с коротким периодом.

При анализе, очевидно, что с увеличением жесткости пружины амплитуда уменьшается, а частота колебаний возрастает. Это значит, что система становится жестче, и блок двигается быстрее, но с меньшей амплитудой.

Таким образом, значение жесткости пружины критично влияет на характер движения системы. Разные значения жесткости приводят к изменениям в амплитуде, частоте и периоде колебаний блока, что важно учитывать при расчетах и моделировании.

Видео:Решение задач на блокиСкачать

🔧 Применение теоретических знаний в практике и инженерии

Одной из ключевых областей применения теоретических знаний о движении блока, привязанного к стене пружиной, является инженерная практика. Инженеры, работающие в области механики и упругости материалов, часто сталкиваются с задачами, требующими точных расчетов сил упругости и деформаций систем.

На практике инженеры используют закон Гука и формулы, разработанные на основе жесткости пружины и массы блока, для проектирования и анализа различных механических систем. Это позволяет предсказывать поведение материалов и конструкций в условиях различных нагрузок и внешних воздействий.

Инженеры также используют теоретические расчеты для оптимизации конструкций, увеличения эффективности систем и уменьшения рисков возможных поломок и деформаций. Такой подход помогает создавать более надежные и долговечные инженерные решения, а также экономить время и ресурсы при проектировании и эксплуатации.

Видео:Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

📚 Рекомендуемые ресурсы для углубленного изучения темы

Для тех, кто хочет более глубоко понять принципы и расчеты, связанные с движением блока, прикрепленного к пружине, полезно обратить внимание на следующие ресурсы:

• Книга: «Физика: Введение в механику» от Ричарда Фейнмана — обширное руководство по механике, включая детали закона Гука и сил упругости.
• Веб-ресурсы: Сайт Khan Academy предлагает бесплатные уроки и практические задания по физике, включая разделы о пружинах и законе Гука.
• Научные статьи: Исследования в журналах «Physics Today» и «Journal of Applied Mechanics» содержат актуальные работы о применении теоретических концепций в инженерной практике.

Использование этих ресурсов поможет углубить знания и приложить теоретические аспекты к реальным ситуациям, связанным с движением пружинных систем.

📸 Видео

#5 Занятие. Движение тела по окружности с постоянной скоростью. Решение задач по физике. КинематикаСкачать

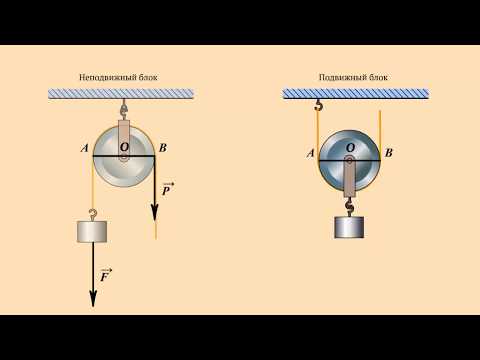
Урок 2. Неподвижные и подвижные блоки. Теория. ЕГЭСкачать

Блок и воротСкачать

Урок 74. Равновесие тела с закрепленной осью вращенияСкачать

На горизонтальном столе находится брусок массой М=1 кг, соединённый невесомой нерастяжимой - №33528Скачать

Простая рама. Определение частот и форм собственных колебаний системы с сосредоточенными массамиСкачать

Применение правила рычага к блокамСкачать

004-017 Как на веревке, которая выдерживает груз массой 200 кг, можно поднимать груз массой 400 кг?Скачать

Урок 83 (осн). Задачи на блокиСкачать

Физика. Задача о грузах, подвешенных на блоке.Скачать

Урок 82 (осн). БлокиСкачать

Брусок массой m = 2 кг движется поступательно по горизонтальной плоскости под действием - №Скачать