Коэффициент полезного действия

Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или затраченную работу A_з и полезную работу A_п. Если, например, наша цель — поднять груз массой m на высоту h, то полезная работа — это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:

    A_п = F_тh = mgh.      (24.1)

Если же мы применяем для подъема груза блок или какой-либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:

A_з > A_п

Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.

Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.

Сокращенное обозначение коэффициента полезного действия — КПД.

Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.

Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой η (читается «эта»):

    η =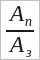* 100%    (24.2)

Поскольку числитель A_п в этой формуле всегда меньше знаменателя A_з, то КПД всегда оказывается меньше 1 (или 100%).

Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:

    A_з ≈ A_п     (24.3)

Следует помнить, что выигрыша в работе с помощью простого механизма получить нельзя.

Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:

    F₁s₁ ≈ F₂s₂     (24.4)

Отсюда следует, что,

выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.

Этот закон называют «золотым правилом» механики. Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.

«Золотое правило» механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.

Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.

1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается «золотое правило» механики? Кто его автор? 6. Приведите примеры проявления «золотого правила» механики при использовании различных простых механизмов.