Простые механизмы

В предыдущем параграфе вы познакомились с рычагом – механическим устройством для перемещения грузов за счет выигрыша в силе. Используя неравноплечий рычаг, можно, приложив небольшую силу, переместить тело значительной массы. Рычаг был одним из первых механизмов, известных людям с древних времен. Существуют и другие механические устройства, которые позволяют изменять не только модуль силы, но и ее направление. Такие устройства называют простыми механизмами.

Механические устройства, с помощью которых можно изменять на- правление и модуль силы, называют простыми механизмами.

Рассмотрим некоторые виды простых механизмов.

Блоком называют устройство, представляющее собой колесо с желобом, по которому пропускают веревку, трос или цепь. Принято различать два вида блоков: неподвижный и подвижный.

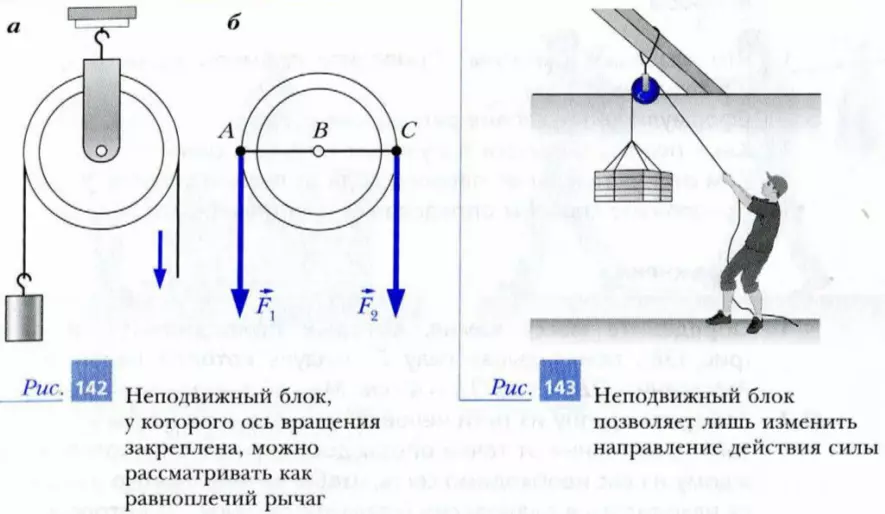
У неподвижного блока (рис. 142, а) ось вращения закреплена. Неподвижный блок действует как равноплечий рычаг относительно оси B вращения колеса (рис. 142, б). Поэтому такой блок не дает выигрыша в силе. Его используют только для того, чтобы изменить направление прикладываемой силы (рис. 143).

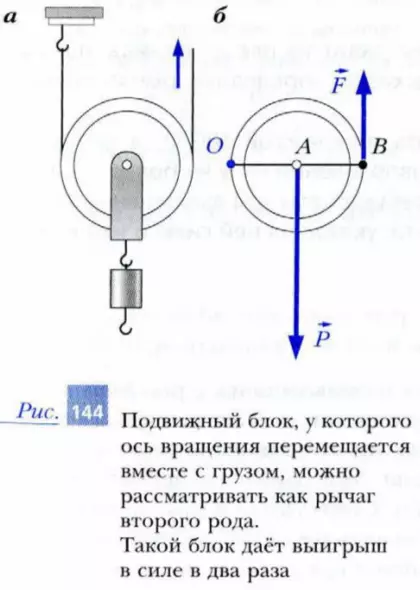
У подвижного блока (рис. 144, а) ось вращения перемещается вместе с грузом. Этот блок дает выигрыш в силе в дои раза. Действительно, подвижный блок можно рассматривать как рычаг второго рода относительно точки O. В этой точке веревка касается блока со стороны ее закрепленного конца (рис. 144, б). Плечо OB прикладываемой силы F в два раза больше плеча OA веса P груза. Поэтому, исходя из условия равновесия, модуль прикладываемой силы будет в дна раза меньше модуля веса груза.

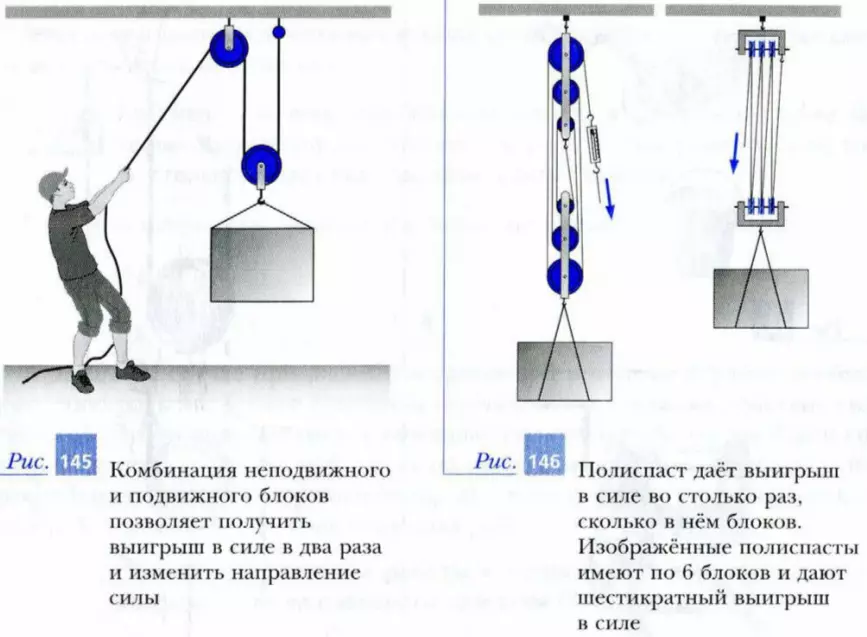
На практике часто используют комбинацию подвижного и неподвижного блоков (рис. 145). Такое сочетание блоков позволяет изменить направление силы и при этом получить двукратный выигрыш в силе. Еще больший выигрыш в силе можно получить при использовании системы блоков, которую называют полиспастом (рис. 146). Полиспаст представляет собой комбинацию подвижного и неподвижного блоков, которая повторяется несколько раз. При этом все неподвижные блоки, как правило, собраны в одну обойму, а все подвижные блоки – в другую, подвижную обойму.

Простым механизмом является и такое устройство, как ворот (рис. 147). Ворот состоит из цилиндра и прикрепленной к торцу цилиндра рукоятки. Цилиндр может вращаться вокруг неподвижной оси. Обычно ворот применяют для подъема грузов из колодцев, шахт и т. п.

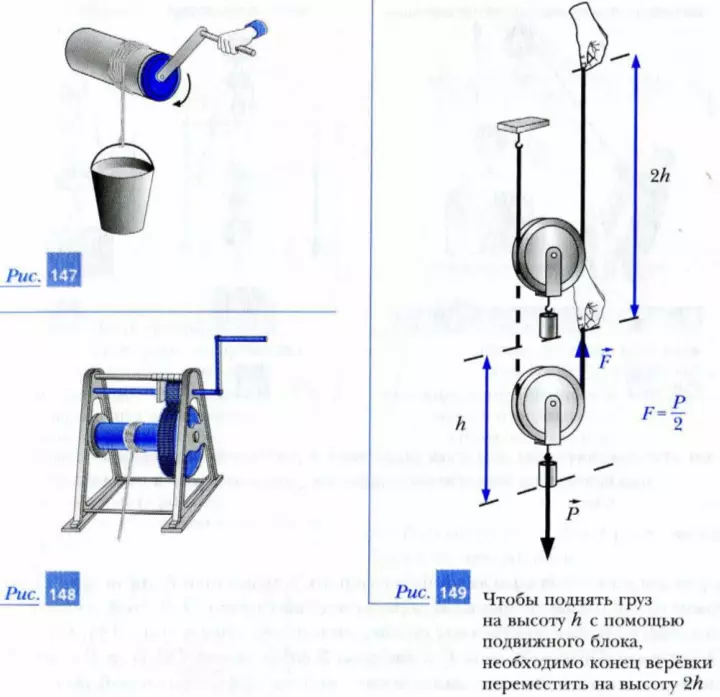
К простым механизмам относятся и различные виды лебедок. Одна из них показана на рис.148. Она представляет собой комбинацию двух воротов, соединенных через зубчатые колеса.

Отметим, что использование простых механизмов, дающих выигрыш в силе в несколько раз, приводит к проигрышу в перемещении во столько же раз. Например, при использовании подвижного блока, выигрывая в два раза в силе (рис. 149), мы в два раза проигрываем в перемещении. Для того чтобы поднять груз на высоту h, нам необходимо переместить конец веревки на расстояние 2h. Поэтому совершенная нами работа (затраченная работа) A_з в идеальном случае (т. е. без учета веса блока, веревки и действия сил трения в оси блока) при равномерном подъеме груза будет всегда равна полезной работе A_п по перемещению груза:

A_з = A_п

Этот закон называют «золотым правилом механики». Он справедлив для всех простых механизмов.

При использовании простых механизмов в идеальном случае затраченная работа равна полезной работе. Выигрывая в силе, мы во столько же раз проигрываем в перемещении.

В данном случае для подвижного блока мы имеем:

A_п = P · h,
A_з = F · 2h = P/2 · 2h = P · h

В реальном случае при расчете затраченной и полезной работ необходимо учитывать вес блоков (рычагов, веревок и т. п.), а также действие сил трения. Так, при подъеме груза с помощью подвижного блока мы будем совершать дополнительную работу по подъему самого блока, веревки и по преодолению силы трения в оси блока. Поэтому в реальности затраченная работа A_з всегда будет больше полезной работы: A_з > A_п.

Отношение полезной работы к затраченной работе называют коэффициентом полезного действия (КПД) механизма.

КПД = A_п / A_з

Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой η (читается «эта»).

η = A_п / A_з · 100%

В реальном случае КПД всегда меньше 1 (η < 100 %).

Итоги

Механические устройства, с помощью которых можно изменять направление и модуль силы, называют простыми механизмами.

В идеальном случае при использовании простых механизмов, выигрывая в силе, мы во столько же раз проигрываем в перемещении. Поэтому затраченная нами работа А_з равна полезной работе A_п. Этот закон называют «золотым правилом механики». В реальном случае затраченная работа A_з всегда будет больше полезной работы A_п.

Отношение полезной работы к затраченной работе называют коэффициентом полезного действия (КПД) механизма.

КПД = A_п / A_з

Вопросы

1. Что называют простыми механизмами? Приведите примеры таких механизмов.
2. Какие виды блоков вы знаете?
3. Для чего используют неподвижный блок?
4. Какой выигрыш в силе дает подвижный блок?
5. Сформулируйте «золотое правило механики».
6. Что называют коэффициентом полезного действия (КПД)? Может ли КПД механизма быть больше единицы (больше 100 %)?

Упражнения

1. Какой выигрыш в силе дает ворот, изображенный на рис. 147, в идеальном случае, если радиус его цилиндра равен 10 см, а длина рукоятки составляет 50 см?
2. Какой выигрыш в силе в идеальном случае даст полиспаст, если в нем будет 4 подвижных блока?
3. Определите массу ведра с водой, которое можно поднять в идеальном случае с помощью ворота, изображенного на рис. 147, если приложить к ручке силу 300 Н. Длина ручки равна 50 см, а радиус цилиндра – 10 см.
4. Обоснуйте утверждение, что в вороте используется принцип действия рычагов первого и второго рода. Сделайте чертеж, на котором изобразите действующие на ворот силы и их плечи.
5. Определите массу камня, равномерно поднимаемого с помощью полиспаста, изображенного на рис. 146, если показание динамометра равно 100 Н.
6. Определите КПД ворота (см. рис. 147) в идеальном случае, если к его ручке прикладывают силу 300 Н, а масса равномерно поднимаемого груза – 75 кг. Длина ручки равна 50 см, радиус цилиндра – 10 см.
7. Определите КПД полиспаста, изображенного на рис. 146, если модуль приложенной силы равен 200 Н, а масса равномерно поднимаемого камня равна 90 кг.