Сила упругости

Как вы уже знаете, при действии на точечное тело силы оно приобретает ускорение в инерциальной системе отсчета. Если же сумма всех сил, действующих на точечное тело, равна нулю, то его ускорение в ИСО равно нулю. Точно так же в ИСО будет равно нулю ускорение точечного тела, если на него не действуют никакие силы. Причем отличить эти две ситуации и сказать, какая из них имеет место, невозможно. Однако отличие может проявиться, если тело не является точечным, а действующие силы приложены к разным точкам этого тела.

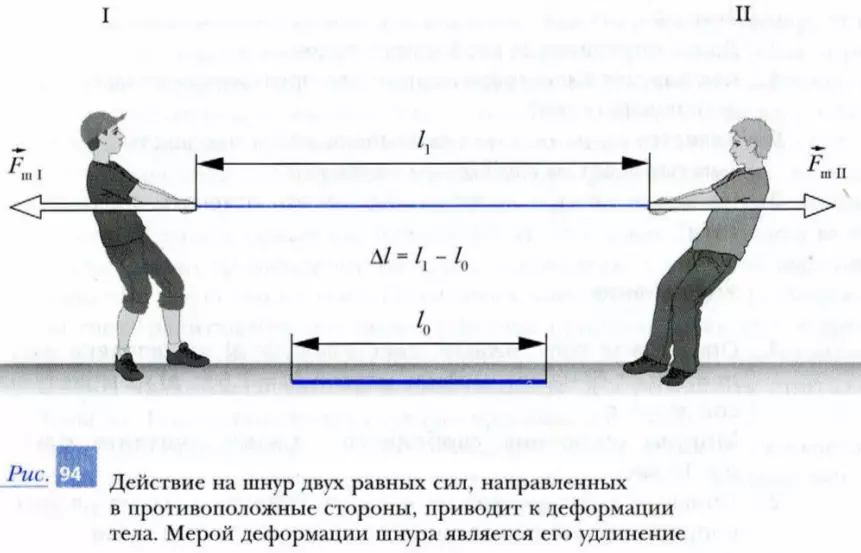
Поясним сказанное на примере. Пусть два мальчика возьмут за концы лежащий на полу очень легкий резиновый шнур длиной l₀ и начнут постепенно его растягивать в противоположные стороны, прикладывая к нему все большие и большие усилия (рис. 94). Обозначим силу, с которой действует первый мальчик на шнур, F_шI, а силу действия на шнур второго мальчика – F_шII. Пусть модули этих сил, возрастая, все время остаются равными друг другу. В этом случае шнур в целом будет оставаться неподвижным относительно Земли, хотя его разные участки начнут постепенно смещаться друг относительно друга по мере увеличения усилий со стороны мальчиков. Длина шнура будет постепенно увеличиваться. Про растянутый шнур говорят, что он находится в деформированном состоянии, или, более точно, шнур испытывает деформацию растяжения.

Когда модули сил станут достаточно большими, шнур вытянется в «струнку» и его длина станет равной l₁. Таким образом, если к протяженному телу в разных его точках приложены две равные по модулю и противоположно направленные силы, то размеры тела изменяются, в нем возникают деформации.

Деформацию растяжения шнура характеризуют его удлинением – величиной Δl = l₁ - l₀.

По третьему закону Ньютона в любой момент времени со стороны шнура на мальчиков будут действовать силы F_Iш и F_IIш. По модулю они будут равны силам действия мальчиков: F_Iш = -F_шI, и F_IIш = -F_шII.

Силы, действующие со стороны шнура, называют силами упругости. Деформированный шнур «стягивает» мальчиков, стремясь вернуться в недеформированное, исходное состояние (рис. 95).

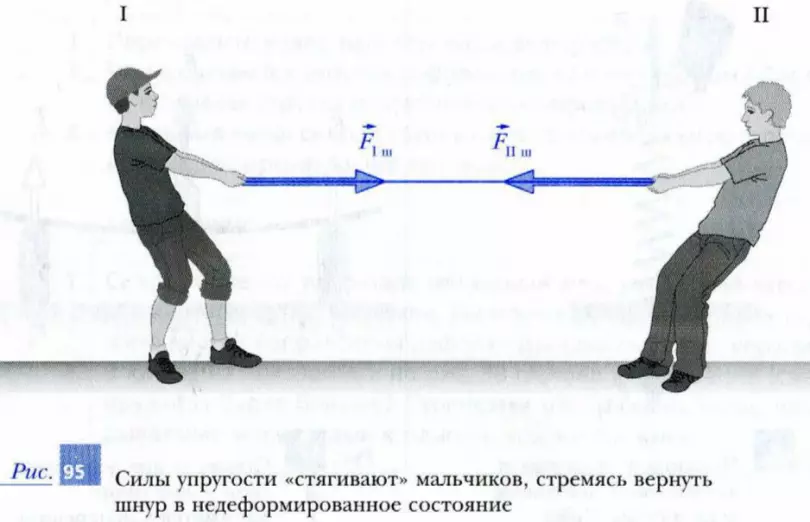
Деформированное тело стремится вернуться в исходное состояние и действует на деформирующие его тела силами упругости.

Наряду с деформацией растяжения могут существовать деформации и других видов. Например, при сжатии пружины ее длина уменьшается, возникает деформация сжатия, и силы упругости стремятся «растолкнуть» вызывающие сжатие тела (рис. 96). При изгибе стержня возникает деформация изгиба (рис. 97) и т. п.

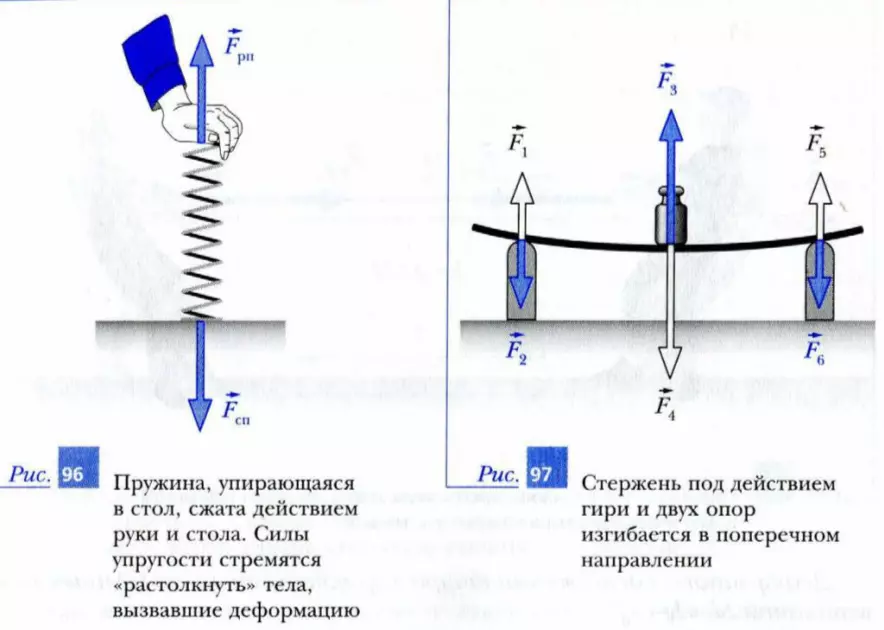
Если после исчезновения сил, вызывающих те или иные деформации, тело возвращается в исходное (недеформированное) состояние, то такие деформации называют упругими. Если же тело не возвращается в исходное состояние, то говорят, что деформации тела были пластическими (неупругими). Пластические деформации имеют место, например, при изгибании, ковке, штамповке изделий из металлов и пластмасс, лепке из глины и пластилина.

Итоги

Если к разным точкам протяженного тела приложены разные (по направлению и модулю) силы, то в теле возникают деформации.

Деформированное тело стремится вернуться в исходное состояние и действует на деформирующие его тела силами упругости.

Если после исчезновения деформирующих сил тело возвращается в исходное (недеформированное) состояние, то такие деформации называют упругими.

Если же после исчезновения деформирующих сил тело не принимает первоначальной формы, то деформации тела называют неупругими или пластическими.

Деформации могут быть разных видов: растяжение, сжатие, изгиб и другие.

Вопросы

1. Перечислите известные вам виды деформаций.
2. Чем отличаются упругие деформации от пластических? Приведите примеры упругих и пластических деформаций.
3. Как называются силы, с которыми деформированное тело действует на деформирующие его тела?

Упражнения

1. Сожмите между ладонями теннисный мяч, удерживая его неподвижно относительно Земли. Зарисуйте схему эксперимента, укажите на ней направления деформирующих сил и сил упругости.

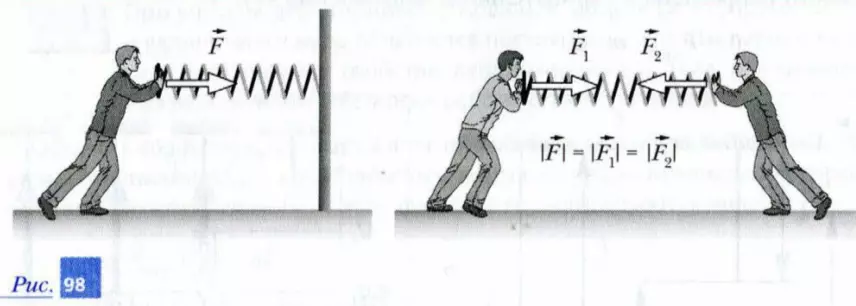
2. В каком из показанных на рис. 98 случаев деформация (сжатие) пружины будет больше? Стрелками изображены силы, прикладываемые мальчиками к одной и той же пружине.

3. Как соотносятся модули сил, показанных на рис. 97:
а) F₁ и F₂; б) F₃ и F₄; в) F₅ и F₆?
Равны ли суммы сил F₁ + F₄ + F₅ и F₂ + F₃ + F₆?
Указание: стержень считать неподвижным относительно Земли, массой стержня пренебречь.