Закон сохранения энергии в механике

1. Когда механическая энергия сохраняется?

Из курса физики основной школы вы уже знаете, что
сумму кинетической и потенциальной энергий называют полной механической энергией.
Докажем, что
полная механическая энергия замкнутой системы тел, взаимодействующих посредством сил упругости и тяготения, сохраняется, то есть ее изменение равно нулю:

∆(E_k + E_p) = 0.     (1)

Это утверждение называют законом сохранения энергии в механике. Его доказательство мы получим как обобщение примера, рассмотрение которого поможет вам и при решении задач.

Возьмем шар массой m, подвешенный к легкой пружине, которая может вращаться вокруг горизонтальной оси O (рис. 31.1).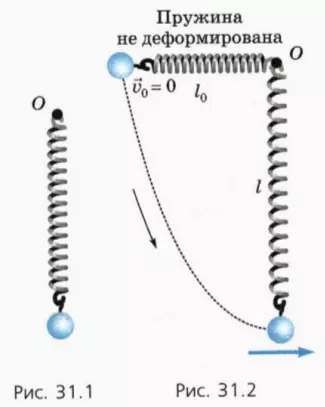

Отклоним шар так, чтобы пружина была горизонтальна и не деформирована (рис. 31.2), и отпустим его без толчка. Шар начнет двигаться вниз по некоторой кривой, а пружина при этом будет растягиваться.

Обозначим l длину пружины в тот момент, когда шар находится в нижней точке траектории. При этом удлинение пружины x = l – l₀, где l₀ – длина недеформированной пружины. Чему равна при этом кинетическая энергия шара?

Ответ на этот вопрос мы найдем с помощью теоремы об изменении кинетической энергии, которая является следствием второго закона Ньютона. Согласно этой теореме изменение кинетической энергии шара равно алгебраической сумме работ всех приложенных к нему сил.

На шар действуют сила тяжести и сила упругости пружины. При движении от верхней точки до нижней шар переместился вниз на расстояние l, а деформация пружины стала равной x.

? 1. Чему равна работа силы тяжести при движении шара от верхней точки до нижней?

? 2. Чему равна при этом работа силы упругости?

? 3. Чему равна алгебраическая сумма работы силы тяжести и силы упругости?

Выполнив эти задания, вы увидите, что изменение кинетической энергии шара выражается формулой

E_k2 – E_k1 = mgl – (kx²)/2.     (2)

Найдем теперь изменение потенциальной энергии системы «шар + пружина + Земля». По определению потенциальной энергии ее изменение равно взятой со знаком минус суммарной работе сил упругости и тяготения (см. § 30). Выражение именно для этой работы и стоит в правой части формулы (2). Поэтому

E_p2 – E_p1 = –(mgl – (kx²)/2).     (3)

Сравнивая уравнения (2) и (3), мы видим, что потенциальная энергия системы уменьшилась ровно настолько же, насколько увеличилась кинетическая энергия шара! Поэтому полная механическая энергия системы сохраняется:

E_k2 + E_p2 = E_k1 + E_p1.     (4)

Нетрудно заметить, что в приведенном примере полная механическая энергия системы сохраняется благодаря тому, что увеличение кинетической энергии и уменьшение потенциальной равно работе одних и тех же сил упругости и тяготения, действующих между телами системы.

На этом частном примере мы убедились, что полная механическая энергия системы тел, между которыми действуют силы упругости или тяготения, сохраняется. А теперь заметим, что все использованные в этом примере аргументы можно привести по отношению к любой замкнутой системе тел, между которыми действуют только силы упругости и тяготения. Отсюда и следует закон сохранения энергии в механике.

Рассмотрим примеры применения этого закона.

? 4. Небольшой шар массой m висит на легком стержне длиной l (рис. 31.3). Стержень может без трения вращаться вокруг точки подвеса O. Шару сообщают начальную горизонтальную скорость ₀, в результате чего стержень с шаром начинает вращаться вокруг точки O.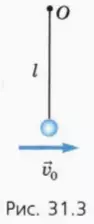

а) Какие слова в условии позволяют считать, в, что полная механическая энергия шара сохраняется?
б) Чему равна работа силы тяжести за время, в течение которого шар движется от нижней точки до верхней?
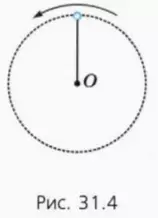
в) Чему равна кинетическая энергия шара в верхней точке (рис. 31.4)?
г) Чему равна скорость шара в верхней точке?

? 5. К недеформированной пружине жесткостью k подвешивают шар массой m и отпускают без толчка (рис. 31. 5, а). Сопротивлением воздуха можно пренебречь.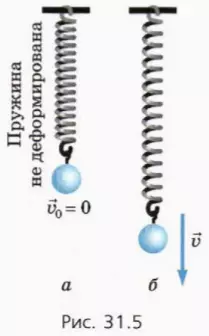

а) Объясните, почему в данном случае можно использовать закон сохранения энергии в механике.
б) Какое расстояние пройдет шар до положения равновесия (рис. 31.5, б)?
в) Остановится ли шар в положении равновесия? Поясните свой ответ.
г) Насколько уменьшилась потенциальная энергия шара при движении к положению равновесия?
д) Насколько увеличилась потенциальная энергия пружины за это же время?
е) Как изменилась суммарная потенциальная энергия системы за это же время?
ж) Чему равна кинетическая энергия шара при прохождении положения равновесия?
з) Как изменилась кинетическая энергия шара за время, в течение которого шар двигался от начального положения до нижней точки своей траектории?
и) Как изменилась суммарная потенциальная энергия системы за то же время?

2. Изменение механической энергии вследствие трения

Рассмотрим случай, когда между телами системы действуют силы трения. Вернемся к примеру, рассмотренному в § 28.

Поставим опыт
Толкнем лежащий на столе брусок (рис. 31.6, а). Он будет скользить по столу и остановится, пройдя некоторое расстояние (рис. 31.6, б).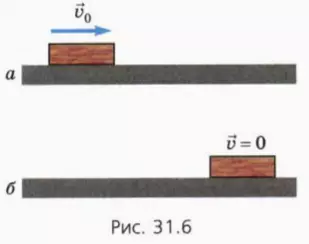

Однако механическая энергия, полученная бруском при толчке, не пропала бесследно! Брусок и стол вследствие трения нагрелись, а при нагревании, как вы уже знаете из курса физики основной школы, увеличивается внутренняя энергия тел.

На примере следующего задания вы увидите, что во внутреннюю энергию может превращаться не только кинетическая, но и потенциальная энергия.

? 6. Брусок соскальзывает с наклонной плоскости с постоянной скоростью.
а) Как изменяется кинетическая энергия бруска?
б) Как изменяется потенциальная энергия бруска?
в) Как изменяется полная механическая энергия бруска?

Итак, в результате трения происходит превращение энергии: механическая энергия превращается во внутреннюю. Однако это превращение энергии существенно отличается от взаимного превращения кинетической и потенциальной энергии.

Важнейшее свойство взаимных превращений кинетической и потенциальной энергии состоит в том, что они обратимы.

Такие превращения энергии происходят, например, при колебаниях подвешенного на нити шара.

Когда подвешенный на нити шар движется к положению равновесия, его потенциальная энергия превращается в кинетическую (рис. 31.7, а).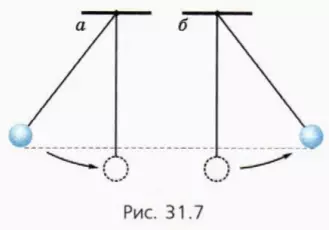

Но когда, пройдя положение равновесия, шар поднимается, его кинетическая энергия превращается снова в потенциальную. И если можно пренебречь сопротивлением воздуха, то потенциальная энергия вернется к начальному значению: шар поднимется до начальной высоты (рис. 31.7, б).

Превращение же энергии из механической во внутреннюю в значительной степени необратимо. Например, если толкнуть лежащий на столе брусок, он будет скользить по столу и остановится, пройдя некоторое расстояние.

Обратный же процесс, при котором лежащий на столе брусок (рис. 31.8, а) вдруг начал бы двигаться с возрастающей скоростью (рис. 31.8, б), невозможен. Такое «чудо» можно увидеть только в кино при «обратном показе».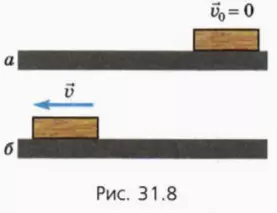

? 7. Приведите другие примеры обратимых и необратимых процессов. В каких примерах механическая энергия сохраняется?

Найдем изменение полной механической энергии системы тел, обусловленное действием сил трения.

Согласно теореме об изменении кинетической энергии оно равно суммарной работе всех сил – упругости, тяготения и трения. Если обозначить суммарную работу сил упругости и тяготения A_{упр.тяг}, то можно записать:
E_k2 – E_k1 = A_{упр.тяг} + A_тр.     (5)
Изменение же потенциальной энергии равно работе только сил упругости и тяготения, взятой со знаком минус:
E_p2 – E_p1 = –A_{упр.тяг}.     (6)
Сложим уравнения (5) и (6). Мы получим:
∆(E_k + E_p) = A_тр.     (7)
Итак,
изменение полной механической энергии замкнутой системы тел равно работе сил трения, действующих между телами системы.

Суммарная работа сил трения всегда отрицательна. (Мы не рассматриваем работу силы трения покоя.) Это – следствие необратимости процессов, в которых механическая энергия переходит во внутреннюю. Подробнее мы рассмотрим их в главе «Термодинамика».

Поскольку суммарная работа сил трения отрицательна, из уравнения (7) следует, что механическая энергия замкнутой системы тел вследствие трения всегда уменьшается.

? 8. В мягкий песок с высоты 2 м падает металлический шар массой 10 кг. В результате падения шар углубился в песок на 50 см.
а) Чему равно изменение полной механической энергии шара?
б) Чему равна работа силы сопротивления песка?
в) Чему равна средняя сила сопротивления песка?

Дополнительные вопросы и задания

9. Шар массой 1 кг бросили вертикально вверх со скоростью 10 м/с. Считайте, что сопротивлением воздуха можно пренебречь. За нулевой уровень потенциальной энергии шара примите его начальное положение.
а) Чему равна полная механическая энергия шара?
б) На какой высоте кинетическая энергия шара равна нулю?
в) На какой высоте значение кинетической энергии шара уменьшилось в 2 раза по сравнению с начальным?
г) На какой высоте кинетическая энергия шара равна его потенциальной энергии?
д) На какой высоте кинетическая энергия шара в 3 раза больше потенциальной?
е) На какой высоте потенциальная энергия шара в 4 раза больше кинетической?

10. Камень массой 200 г бросили с высоты 10 м над уровнем земли с начальной скоростью 5 м/с, направленной вверх под углом 30º к горизонту. Считайте, что сопротивлением воздуха можно пренебречь. За нулевой уровень потенциальной энергии камня примите уровень земли.
а) Чему была равна кинетическая энергия камня, когда он второй раз находился на высоте 10 м?
б) Чему была равна кинетическая энергия камня непосредственно перед ударом о землю?
в) Чему была равна скорость камня непосредственно перед ударом о землю?
г) Есть ли в условии лишние данные?

11. Тело брошено с поверхности земли под углом а к горизонту. За нулевой уровень потенциальной энергии тела примите уровень земли. Считайте, что сопротивлением воздуха можно пренебречь.
а) Чему равно отношение кинетической энергии тела в верхней точке траектории к его начальной кинетической энергии?
б) Чему равен угол α, если в верхней точке траектории кинетическая энергия тела равна его потенциальной энергии?
в) Чему равен угол α, если в верхней точке траектории кинетическая энергия тела в 3 раза меньше его потенциальной энергии?

12. На концах легкого стержня длиной l укреплены небольшие шары массой m и M, причем M > m (рис. 31.9, а). Стержень может вращаться без трения вокруг горизонтальной оси, проходящей через его середину. Стержень с шарами приводят в горизонтальное положение (рис. 31.9, б) и отпускают без толчка.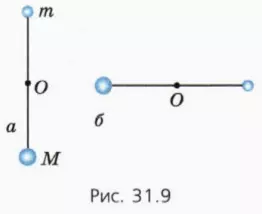

а) Чему будет равна суммарная работа силы тяжести при движении системы к положению равновесия?
б) Чему будет равна суммарная кинетическая энергия шаров в момент, когда система будет проходить положение равновесия?
в) Какова будет скорость шаров в момент, когда система будет проходить положение равновесия?

13. Мяч массой 200 г брошен вертикально вверх с уровня земли со скоростью 20 м/с. Он достиг максимальной высоты 10 м, после чего падал вниз, и его скорость непосредствен- но перед ударом о землю была равна 10 м/с.
а) Чему равна полная механическая энергия мяча в начальный момент?
б) Чему равна полная механическая энергия мяча в верхней точке траектории?
в) Чему равна работа силы сопротивления воздуха, действующей на мяч при подъеме?
г) Чему равен модуль средней силы сопротивления воздуха, действующей на мяч при подъеме?
д) Чему равна полная механическая энергия мяча непосредственно перед ударом о землю?
е) Чему равна работа силы сопротивления воздуха, действующей на мяч при спуске?
ж) Чему равен модуль средней силы сопротивления воздуха, действующей на мяч при спуске?
з) Почему средняя сила сопротивления воздуха, действующая на мяч при спуске, меньше, чем при подъеме?
Подсказка. Сила сопротивления воздуха возрастает при увеличении скорости.

14. Брусок массой 250 г скользит по гладкому столу со скоростью 2 м/с и сталкивается с прикрепленной к стене горизонтальной пружиной жесткостью 200 Н/м (рис. 31.10).

а) Чему равна начальная полная механическая энергия системы «брусок + пружина»?
б) Чему равна потенциальная энергия пружины в момент, когда ее деформация максимальна?
в) Чему равна максимальная деформация пружины?
г) Чему равна скорость бруска в момент, когда деформация пружины в 2 раза меньше максимальной?
д) Чему равна скорость бруска после взаимодействия с пружиной?

15. Горизонтальная пружина жесткостью 200 Н/м прижата к стене бруском массой 50 г (рис. 31.11). В начальный момент деформация пружины равна по модулю 3 см, а брусок покоится. Брусок отпускают без толчка, и он скользит по столу, пройдя до остановки 45 см.

а) Чему равна начальная полная механическая энергия системы «брусок + пружина»?
б) Чему равна конечная полная механическая энергия системы «брусок + пружина»?
в) Чему равна работа силы трения, действовавшей на брусок со стороны стола?
г) Чему равна сила трения между бруском и столом?
д) Чему равен коэффициент трения между бруском и столом?