Разрывы и столкновения
1. Разрыв летящего снаряда
В этом параграфе мы будем предполагать, что сопротивлением воздуха можно пренебречь.
? 1. Выпущенный вертикально вверх снаряд разорвался в верхней точке траектории на два осколка массой m1 и m2 (рис. 32.1). Чему равно отношение скоростей осколков после разрыва? (Под скоростями до и после разрыва или столкновения здесь и далее мы понимаем скорости непосредственно до и сразу после разрыва или столкновения.)
Подсказка. Скорость снаряда в верхней точке траектории равна нулю. Воспользуйтесь законом сохранения импульса.
? 2. Тело, находящееся на высоте h, движется со скоростью, равной по модулю v0. Чему равен модуль скорости тела при падении на землю?
Подсказка. Воспользуйтесь законом сохранения энергии.
? 3. Снаряд, выпущенный вертикально вверх с начальной скоростью v0, разорвался в верхней точке траектории на два осколка, модули скорости которых равны v10 и v20. Каковы скорости осколков при падении на землю?
Подсказка. Высоту, на которой разорвался снаряд, можно связать с его начальной скоростью.
? 4. Снаряд, выпущенный вертикально вверх с начальной скоростью v0, разорвался в верхней точке траектории на два осколка, которые упали на землю со скоростями v1 и v2.
а) Чему равно отношение скоростей осколков после разрыва?
б) Чему равно отношение масс осколков?
? 5. Снаряд, выпущенный из пушки вертикально вверх, разорвался в верхней точке траектории на два осколка, скорости которых после разрыва направлены горизонтально. Первый осколок упал на расстоянии 1 км от пушки, а второй – на расстоянии 500 м.
а) Как связаны скорости v10 и v20 осколков после разрыва?
б) Чему равно отношение масс осколков?
? 6. Снаряд, выпущенный из пушки со скоростью v0 под углом α к горизонту, разорвался в верхней точке траектории на два осколка равной массы. Скорости осколков после разрыва направлены горизонтально. Первый из них упал недалеко от пушки.
а) Как связана скорость первого осколка после разрыва со скоростью снаряда перед разрывом?
б) Как связана скорость второго осколка после разрыва со скоростью снаряда перед разрывом?
в) На каком расстоянии от пушки упал бы снаряд, если бы он не разорвался?
г) На каком расстоянии от пушки упал второй осколок?
2. Упругие столкновения
Столкновение тел называют упругим, если механическая энергия тел в результате столкновения не изменяется. Таким можно считать, например, рассмотренное выше столкновение бильярдных шаров.
Столкновение двух тел называют центральным, если их скорости до столкновения и после него направлены вдоль одной прямой.
Пусть шар массой m1, движущийся со скоростью  1, налетает на покоящийся шар массой m2. Обозначим
1, налетает на покоящийся шар массой m2. Обозначим 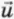 1 и
1 и 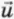 2 скорости шаров после упругого центрального столкновения. Направим ось x по направлению скорости
2 скорости шаров после упругого центрального столкновения. Направим ось x по направлению скорости 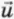 1 налетающего шара. (В таком случае проекция скорости
1 налетающего шара. (В таком случае проекция скорости  1 на ось x равна v1. Поэтому для упрощения формул мы пишем v1 вместо v1x.)
1 на ось x равна v1. Поэтому для упрощения формул мы пишем v1 вместо v1x.)
? 7. Объясните смысл следующих уравнений: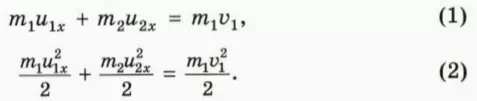
Подсказка. До и после столкновения тела движутся вдоль оси х, поэтому квадраты скоростей равны квадратам проекций скоростей: u12 = u1x2, u22 = u2x2.
Переход и системе двух линейных уравнений
Перепишем уравнения (1) и (2) так, чтобы величины, относящиеся ко второму шару, находились слева от знака равенства, а к первому шару – справа. Кроме того, сократим общий множитель ½. Мы получим: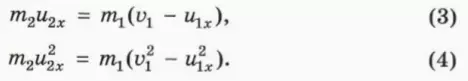
? 8. Объясните, как из этих уравнений получить уравнение
u2x = v1 + u1x. (5)
Подсказка. Если столкновение произошло, то обе части уравнения (3) отличны от нуля. Поэтому можно разделить левую и правую части уравнения (4) соответственно на левую и правую части уравнения (3).
Уравнения (3) и (5) представляют собой систему двух линейных уравнений. Используя эту систему, легко выполнить следующее задание.
? 9. Чему равны проекции скоростей шаров после столкновения?
Из формул, полученных при выполнении этого задания, можно сделать качественные выводы, которые помогут при решении задач.
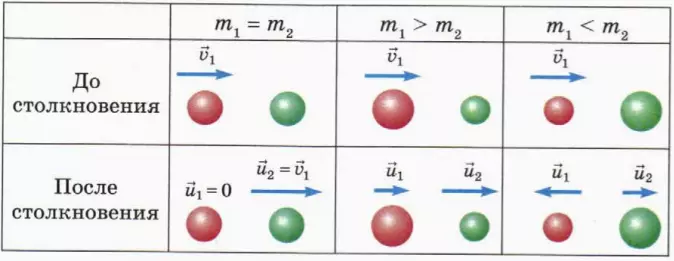
? 10. Шар массой m1 налетает со скоростью  1 на покоящийся шар массой m2. Удар упругий центральный. Используя результаты предыдущего задания, прокомментируйте содержание следующей таблицы.
1 на покоящийся шар массой m2. Удар упругий центральный. Используя результаты предыдущего задания, прокомментируйте содержание следующей таблицы.
? 11. Шар налетел со скоростью 2 м/с на второй покоящийся шар и отскочил назад со скоростью 0,5 м/с. Столкновение было упругим и центральным.
а) С какой скоростью начал двигаться второй шар после столкновения?
б) Чему равно отношение масс шаров?
Подсказка. Воспользуйтесь системой уравнений (3) и (4).
Столкновение подвешенных шаров
Упругие столкновения удобно исследовать с помощью подвешенных на нитях шаров.
Поставим опыт
Подвесим на нитях равной длины несколько одинаковых стальных или костяных шаров (рис. 32.2).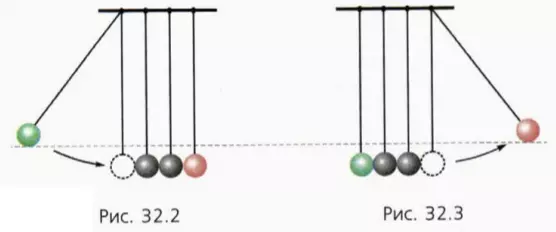
Отведем в сторону крайний левый шар и отпустим. Мы окажемся свидетелями красивого явления. После удара левого шара все шары, кроме крайнего правого, будут находиться в покое, а крайний правый шар отклонится, поднявшись при этом на высоту, равную начальной высоте левого шара (рис. 32.3).
? 12. Объясните описанный опыт, считая столкновение шаров упругим и центральным. Что будет наблюдаться, если отклонить не один, а два или три шара вместе? Проверьте свое предсказание на опыте.
Рассмотрим теперь случай, когда массы подвешенных шаров не равны.
? 13. На вертикальных нитях длиной l = 90 см висят, соприкасаясь, два шарика массой m1 = 20 г и m2 = 40 г. Первый шарик отклонили так, что нить составила угол 60º с вертикалью, и отпустили без толчка (рис. 32.4). Столкновение шаров считайте упругим и центральным.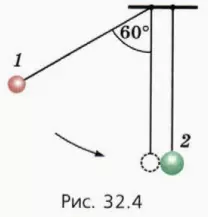
а) Чему равна кинетическая энергия первого шарика перед столкновением?
б) Чему равна скорость первого шарика перед столкновением?
в) Чему равна скорость первого шарика после столкновения?
г) На какую максимальную высоту поднимется первый шарик после столкновения?
д) Чему равна скорость второго шарика после столкновения?
е) На какую максимальную высоту поднимется второй шарик после столкновения?
3. Неупругие столкновения
Неупругим называют столкновение, в результате которого суммарная механическая энергия сталкивающихся тел уменьшается. При этом она обычно переходит во внутреннюю энергию, то есть выделяется некоторое количество теплоты Q.
Максимальное уменьшение механической энергии происходит, когда тела после столкновения движутся как единое целое. Поэтому такое столкновение называют абсолютно неупругим.
Согласно общему закону сохранения энергии, известному вам из курса Физики основной школы, суммарная энергия замкнутой системы тел (включая внутреннюю энергию) сохраняется. Поэтому начальная и конечная механическая энергия, а также выделившееся количество теплоты связаны соотношением
Eмех.нач = Eмех.кон + Q.
? 14. Пластилиновый шарик массой m налетает со скоростью и на такой же покоящийся шарик. После столкновения шарики движутся как единое целое.
а) Чему равна общая скорость шариков после столкновения?
б) Чему равна начальная механическая энергия шариков?
в) Чему равна конечная механическая энергия шариков?
г) Какое количество теплоты Q выделилось в результате столкновения?
Баллистический маятник
Для измерения скорости пули можно выстрелить в подвешенный на нити массивный брусок (рис. 32.5, а) и измерить, на какую максимальную высоту поднимется брусок вместе с застрявшей в нем пулей (рис. 32.5, б).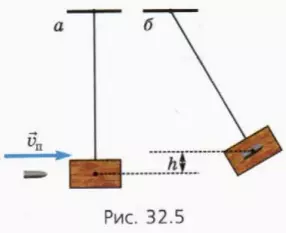
Главное в этой ситуации увидеть, что весь процесс состоит из двух этапов, которые надо рассматривать по отдельности.
1. Столкновение пули с бруском. На этом этапе механическая энергия не сохраняется, потому что столкновение не: упругое. Скорость бруска с пулей сразу после столкновения можно определить с помощью закона сохранения импульса. Время столкновения столь мало, что за это время брусок не успевает заметно отклониться от положения равновесия.
2. Подъем бруска с пулей. На этом этапе механическая энергия сохраняется. Поэтому увеличение потенциальной энергии бруска с пулей при подъеме до максимальной высоты равно их кинетической энергии после столкновения.
? 15. Летящая горизонтально пуля массой m = 10 г попадает в брусок массой M = 1 кг, подвешенный на нити длиной l = 1 м. Пуля застревает в бруске. Скорость пули перед попаданием в брусок vп = 300 м/с.
а) Чему равна начальная кинетическая энергия пули?
б) Чему равна скорость бруска с пулей после столкновения?
в) Чему равна кинетическая энергия бруска с пулей после столкновения?
г) Какое количество теплоты выделилось при столкновении?
д) Каково увеличение потенциальной энергии бруска с пулей при подъеме до максимальной высоты?
е) На какую максимальную высоту поднялся брусок с пулей?
На этом конкретном примере вы увидели, что если масса бруска намного больше массы пули, то почти вся начальная кинетическая энергия пули превращается во внутреннюю энергию! Так всегда происходит при неупругом столкновении тела с покоящимся телом, масса которого намного больше.
Дополнительные вопросы и задания
16. Выпущенный вертикально вверх со скоростью 300 м/с снаряд разорвался в верхней точке траектории на два осколка равной массы. Первый осколок полетел вертикально вниз, а второй – вертикально вверх. Осколки упали на землю с интервалом времени 12 с.
а) Через какой промежуток времени после разрыва второй осколок снова оказался на высоте разрыва?
б) Чему равна скорость осколков относительно земли после разрыва?
в) Чему равно расстояние между осколками через 2 с после разрыва?
г) До какой высоты над землей поднялся второй осколок?
д) С какими скоростями осколки упали на землю?
17. Белый шарик массой 100 г налетает со скоростью 5 м/с на покоящийся черный шарик и в результате упругого центрального удара отскакивает назад со скоростью 3 м/с.
а) Чему равна скорость черного шарика после удара?
б) Чему равна масса черного шарика?
18. В лежащую на гладком льду льдину массой 3 кг попадает камень, летящий горизонтально со скоростью 10 м/с. После удара камень отскакивает обратно со скоростью 2 м/с, а льдина начинает двигаться со скоростью 2 м/с.
а) Чему равна масса камня?
б) Чему равна кинетическая энергия камня до столкновения?
в) Чему равна суммарная кинетическая энергия льдины и камня после столкновения?
г) Какое количество теплоты Q выделилось при ударе?
19. На тележку массой M, движущуюся горизонтально со скоростью v, падает вертикально с высоты h кусок пластилина массой m. Считайте, что столкновение было абсолютно неупругим; трением и сопротивлением воздуха можно пренебречь.
а) Чему равна начальная механическая энергия системы «тележка + пластилин»?
б) Чему равна скорость тележки с пластилином?
в) Чему равна конечная механическая энергия системы «тележка + пластилин»?
г) Какое количество теплоты Q выделилось при ударе?
