Свободное падение и движение тела, брошенного вертикально вверх

1. Свободное падение тела

Закономерности падения тел открыл Галилео Галилей.

Знаменитый опыт с бросанием шаров с наклонной Пизанской башни (рис. 7.1, а) подтвердил его предположение, что если сопротивлением воздуха можно пренебречь, то все тела падают одинаково. Когда с этой башни бросили одновременно пулю и пушечное ядро, они упали практически одновременно (рис. 7.1, б).

Падение тел в условиях, когда сопротивлением воздуха можно пренебречь, называют свободным падением.

Поставим опыт
Свободное падение тел можно наблюдать с помощью так называемой трубки Ньютона. Положим в стеклянную трубку металлический шарик и перышко. Перевернув трубку, мы увидим, что перышко падает медленнее, чем шарик (рис. 7.2, а). Но если откачать из трубки воздух, то шарик и перышко будут падать с одинаковой скоростью (рис. 7.2, б).

Значит, различие в их падении в трубке с воздухом обусловлено только тем, что сопротивление воздуха для перышка играет большую роль.

Галилей установил, что при свободном падении тело движется с постоянным ускорением, Его называют ускорением свободного падения и обозначают . Оно направлено вниз и, как показывают измерения, равно по модулю примерно 9,8 м/с². (В разных точках земной поверхности значения g немного различаются (в пределах 0,5%).)

Из курса физики основной школы вы уже знаете, что ускорение тел при падении обусловлено действием силы тяжести.

При решении задач школьного курса физики (в том числе заданий ЕГЭ) для упрощения принимают g = 10 м/с². Далее мы тоже будем поступать так же, не оговаривая этого особо.

Рассмотрим сначала свободное падение тела без начальной скорости.

В этом и следующих параграфах мы будем рассматривать также движение тела, брошенного вертикально вверх и под углом к горизонту. Поэтому введем сразу систему координат, подходящую для всех этих случаев.

Направим ось x по горизонтали вправо (в этом параграфе она нам пока не понадобится), а ось y – вертикально вверх (рис. 7.3). Начало координат выберем на поверхности земли. Обозначим h начальную высоту тела.

Свободно падающее тело движется с ускорением , и поэтому при равной нулю начальной скорости скорость тела в момент времени t выражается формулой

? 1. Докажите, что зависимость модуля скорости от времени выражается формулой

v = gt.     (2)

Из этой формулы следует, что скорость свободно падающего тела ежесекундно увеличивается примерно на 10 м/с.

? 2. Начертите графики зависимости v_y(t) и v(t) для первых четырех секунд падения тела.

? 3. Свободно падающее без начальной скорости тело упало на землю со скоростью 40 м/с. Сколько времени длилось падение?

Из формул для равноускоренного движения без начальной скорости следует, что

s_y = g_yt²/2. (3)

Отсюда для модуля перемещения получаем:

s = gt²/2. (4)

? 4. Как связан пройденный телом путь с модулем перемещения, если тело свободно падает без начальной скорости?

? 5. Найдите, чему равен путь, пройденный свободно падающим без начальной скорости телом за 1 с, 2 с, 3 с, 4 с. Запомните эти значения пути: они помогут вам устно решать многие задачи.

? 6. Используя результаты предыдущего задания, найдите пути, проходимые свободно падающим телом за первую, вторую, третью и четвертую секунды падения. Разделите значения найденных путей на пять. Заметите ли вы простую закономерность?

? 7. Докажите, что зависимость координаты y тела от времени выражается формулой

y = h – gt²/2.     (5)

Подсказка. Воспользуйтесь формулой (7) из § 6. Перемещение при прямолинейном равноускоренном движении и тем, что начальная координата тела равна h, а начальная скорость тела равна нулю.

На рисунке 7.4 изображен пример графика зависимости y(t) для свободно падающего тела до момента его падения на землю.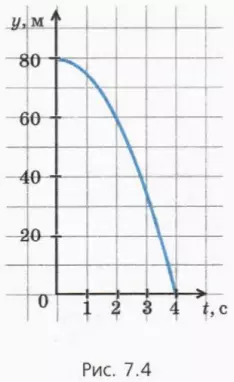

? 8. С помощью рисунка 7.4 проверьте полученные вами ответы на задания 5 и 6.

? 9. Докажите, что время падения тела выражается формулой

Подсказка. Воспользуйтесь тем, что в момент падения на землю координата y тела равна нулю.

? 10. Докажите, что модуль конечной скорости тела vк (непосредственно перед падением на землю)

Подсказка. Воспользуйтесь формулами (2) и (6).

? 11. Чему была бы равна скорость капель, падающих с высоты 2 км, если бы сопротивлением воздуха для них можно было бы пренебречь, то есть они падали бы свободно?

Ответ на этот вопрос удивит вас. Дождь из таких «капелек» был бы губительным, а не живительным. К счастью, атмосфера спасает нас всех: вследствие сопротивления воздуха скорость дождевых капель у поверхности земли не превышает 7–8 м/с.

2. Движение тела, брошенного вертикально вверх

Пусть тело брошено с поверхности земли вертикально вверх с начальной скоростью ₀ (рис. 7.5).

Скорость v_vec тела в момент времени t в векторном виде выражается формулой

В проекциях на ось y:

v_y = v₀ – gt.     (9)

На рисунке 7.6 изображен пример графика зависимости v_y(t) до момента падения тела на землю.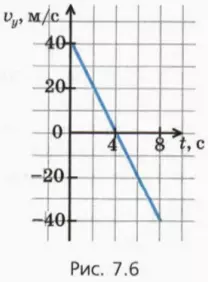

? 12. Определите по графику 7.6, в какой момент времени тело находилось в верхней точке траектории. Какую еще информацию можно извлечь из этого графика?

? 13. Докажите, что время подъема тела до верхней точки траектории можно выразить формулой

t_под = v₀/g.     (10)

Подсказка. Воспользуйтесь тем, что в верхней точке траектории скорость тела равна нулю.

? 14. Докажите, что зависимость координаты у тела от времени выражается формулой

y = v₀t – gt²/2.     (11)

Подсказка. Воспользуйтесь формулой (7) из § 6. Перемещение при прямолинейном равноускоренном движении.

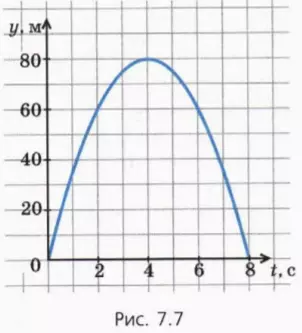
? 15.На рисунке 7.7 изображен график зависимости y(t). Найдите два разных момента времени, когда тело находилось на одной и той же высоте, и момент времени, когда тело находилось в верхней точке траектории. Заметили ли вы какую-то закономерность?

? 16. Докажите, что максимальная высота подъема h выражается формулой

h = v₀²/2g     (12)

Подсказка. Воспользуйтесь формулами (10) и (11) или формулой (9) из § 6. Перемещение при прямолинейном равноускоренном движении.

? 17. Докажите, что конечная скорость тела, брошенного вертикально вверх (то есть скорость тела непосредственно перед падением на землю), равна но модулю его начальной скорости:

v_к = v₀.     (13)

Подсказка. Воспользуйтесь формулами (7) и (12).

? 18. Докажите, что время всего полета

t_пол = 2v₀/g.     (14)
Подсказка. Воспользуйтесь тем, что в момент падения на землю координата y тела становится равной нулю.

? 19. Докажите, что

t_пол = 2t_под.     (15)

Подсказка. Сравните формулы (10) и (14).

Следовательно, подъем тела до верхней точки траектории занимает такое же время, какое занимает последующее падение.

Итак, если можно пренебречь сопротивлением воздуха, то полет тела, брошенного вертикально вверх, естественно разбивается на два этапа, занимающие одинаковое время, – движение вверх и последующее падение вниз в начальную точку.

Каждый из этих этапов представляет собой как бы «обращенный во времени» другой этап. Поэтому если мы снимем на видеокамеру подъем брошенного вверх тела до верхней точки, а потом будем показывать кадры этой видеосъемки в обратном порядке, то зрители будут уверены, что они наблюдают падение тела. И наоборот: показанное в обратном порядке падение тела будет выглядеть в точности как подъем тела, брошенного вертикально вверх.

Этот прием используют в кино: снимают, например, артиста, который спрыгивает с высоты 2–3 м, а потом показывают эту съемку в обратном порядке. И мы восхищаемся героем, легко взлетающим на высоту, недостижимую для рекордсменов.

Используя описанную симметрию между подъемом и спуском тела, брошенного вертикально вверх, вы сможете выполнить следующие задания устно. Полезно также вспомнить, чему равны пути, проходимые свободно падающим телом (задание 4).

? 20. Чему равен путь, который проходит брошенное вертикально вверх тело за последнюю секунду подъема?

? 21. Брошенное вертикально вверх тело побывало на высоте 40 м дважды с интервалом 2 с.
а) Чему равна максимальная высота подъема тела?
б) Чему равна начальная скорость тела?

Дополнительные вопросы и задания

(Во всех заданиях этого параграфа предполагается, что сопротивлением воздуха можно пренебречь.)

22. Тело падает без начальной скорости с высоты 45 м.
а) Сколько времени длится падение?
б) Какое расстояние пролетает тело за вторую секунду?
в) Какое расстояние пролетает тело за последнюю секунду движения?
г) Чему равна конечная скорость тела?

23. Тело падает без начальной скорости с некоторой высоты в течение 2,5 с.
а) Чему равна конечная скорость тела?
б) С какой высоты падало тело?
в) Какое расстояние пролетело тело за последнюю секунду движения?

24. С крыши высокого дома с интервалом 1 с упали две капли.
а) Чему равна скорость первой капли в момент, когда оторвалась вторая капля?
б) Чему равно в этот момент расстояние между каплями?
в) Чему равно расстояние между каплями через 2 с после начала падения второй капли?

25. За последние τ секунд падения без начальной скорости тело пролетело расстояние l. Обозначим начальную высоту тела h, время падения t.
а) Выразите h через g и t.
б) Выразите h – l через g и t – τ.
в) Из полученной системы уравнений выразите h через l, g и τ.
г) Найдите значение h при l = 30 м, τ = 1 с.

26. Синий шарик бросили вертикально вверх с начальной скоростью v0. В момент, когда он достиг высшей точки, из той же начальной точки с той же начальной скоростью бросили красный шарик.
а) Сколько времени продолжался подъем синего шарика?
б) Чему равна максимальная высота подъема синего шарика?
в) Через какое время после бросания красного шарика он столкнулся с движущимся синим?
г) На какой высоте шарики столкнулись?

27. С потолка лифта, поднимающегося равномерно со скоростью vл, оторвался болт. Высота кабины лифта h.
а) В какой системе отсчета удобнее рассматривать движение болта?
б) Сколько времени будет падать болт?

в) Чему равна скорость болта непосредственно перед касанием пола: относительно лифта? относительно земли?