Прямолинейное равномерное движение

1. Скорость

Поставим опыт
Толкнем тележку, находящуюся на горизонтальной поверхности, по которой она может двигаться практически без трения (можно использовать тележку на воздушной подушке).

На рисунке 2. 1 изображены положения тележки через равные промежутки времени. Мы видим, что за разные промежутки времени тележка совершает одинаковые перемещения.

Движение тела, при котором оно за любые равные промежутки времени совершает одинаковые перемещения, называют прямолинейным равномерным.

Это движение вы уже изучали в основной школе. Главная его характеристика – скорость.

Скоростью прямолинейного равномерного движения называют отношение перемещения 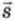к промежутку времени t, за который произошло это перемещение:

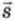= / t     (1)

Скорость – векторная величина. Единицей скорости в СИ является 1 м/с.

? 1. Используя рисунок 2.1, ответьте на следующие вопросы:
а) чему равна скорость тележки в опыте, изображенном на рисунке 2.1, если показаны положения тележки через каждые 0,2 с?
б) какой путь проехала бы тележка за 1 ч, если бы она продолжала двигаться прямолинейно равномерно?
Скорость автомобилей и поездов задают обычно в км/ч, а ракет и искусственных спутников – в км/с.

? 2. Человек идет со скоростью 1 м/с. Какова его скорость в км/ч?

? 3. Автомобиль едет со скоростью 36 км/ч. Какой станет его скорость в км/ч, если она увеличится на 5 м/с?

2. График зависимости координаты от времени

Из определения скорости (1) получаем соотношение между проекциями скорости и перемещения (например, на ось x):

v_x = s_x/t     (2)

Направим ось x вдоль прямой, по которой движется тело, и совместим начало координат с начальным положением тела (оно отмечено светлым кружком на рисунке 2.2). Тогда

s_x = x     (3)

причем s_x положительно, если тело переместилось в положительном направлении оси x (рис. 2.2, а), и отрицательно, если тело переместилось в отрицательном направлении оси x (рис. 2.2, б).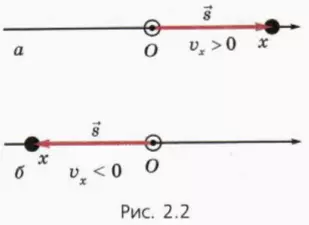

Из формул (2) и (3) получаем в этом случае:

v_x = x/t      (4)

Проекция скорости v_x > 0, когда тело движется в положительном направлении оси x (рис. 2.2, а); если тело движется в отрицательном направлении оси x, то v_x < 0.
Из формулы (4) следует, что зависимость координаты тела от времени выражается формулой

x = v_xt.     (5)

Итак, при прямолинейном равномерном движении из начала координат координата тела x прямо пропорциональна проекции скорости v_x. График такой зависимости — отрезок прямой, один из концов которого совпадает с началом координат. Значение координаты x увеличивается со временем, если v_x > 0, то есть когда тело движется в положительном направлении оси x, и уменьшается со временем, если v_x < 0, то есть когда тело движется в отрицательном направлении оси x.

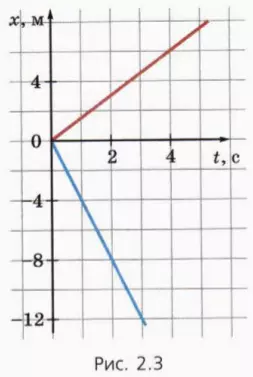
? 4. На рисунке 2.3 изображены графики зависимости координаты от времени для пешехода и велосипедиста.
а) Каким цветом изображен график для пешеходам?
б) В каком направлении оси x ехал велосипедист?
в) Чему равны модули скорости пешехода и велосипедиста?
г) Перенесите графики в тетрадь и добавьте к ним график зависимости координаты от времени для автомобиля, который едет и отрицательном направлении оси x, если модуль его скорости в 5 раз больше модуля скорости велосипедиста.

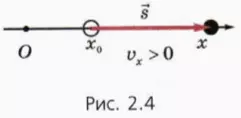
Если в начальный момент тело находилось не в начале координат, а в точке с координатой x₀ (рис. 2.4), то

s_x = s – x     (6)

Поэтому формула (2) принимает вид

v_x = (x – x₀) / t,

откуда следует, что в общем случае

x = x₀ + v_xt.      (7)

Начальное значение координаты x₀ тоже может быть как положительным, так и отрицательным.

? 5. По аналогии с рисунком 2,4 сделайте в тетради чертежи, соответствующие:
а) x₀ < 0; v_x > 0; б) x₀ < 0; v_x < 0.

? 6. На рисунке 2.5 изображены графики зависимости координаты от времени для тела, движущегося вдоль оси x.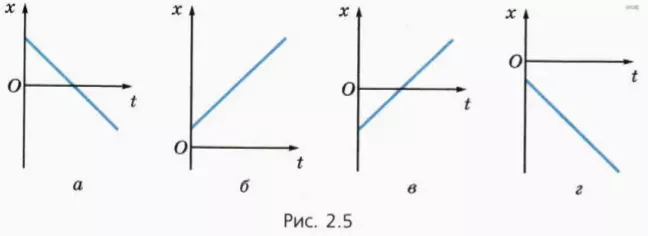

а) Какие графики описывают движение тела в направлении, противоположном направлению оси x?
б) На каких графиках показано, что тело проходит через начало координат?
в) На каких графиках x0 и vx имеют противоположные знаки?

? 7. На рисунке 2.6 изображены графики зависимости координаты от времени для велосипедиста и грузовика.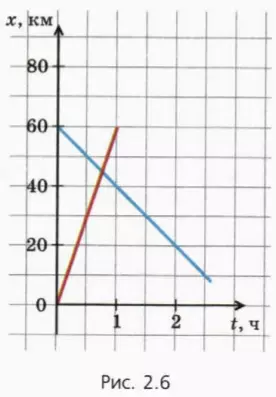

а) Каким цветом изображен график для грузовика?
б) Какому событию соответствует точка пересечения графиков?
в) Какие величины можно определить по этим графикам? Чему они равны?
г) Перенесите эти графики в тетрадь и добавьте к ним график зависимости координаты от времени для легкового автомобиля, который двигался прямолинейно и равномерно, встретился сначала с велосипедистом, а потом – с грузовиком, причем обе эти встречи произошли до того, как грузовик и велосипедист встретились друг с другом. В каком направлении относительно оси х двигался этот легковой автомобиль?

Дополнительные вопросы и задания

8. В 2011 году был установлен очередной мировой рекорд в марафонском беге: дистанцию длиной 42 км 195 м бегун пробежал за 2 ч 3 мин 38 с. А мировой рекорд 2009 года в забеге на 100 м был равен 9,58 с. Приняв, что в обоих случаях бегуны двигались равномерно, найдите скорость каждого из них (в м/с).

9. Искусственный спутник Земли движется по низкой круговой орбите со скоростью, равной примерно 8 км/с. Во сколько раз эта скорость больше скорости самого быстрого гоночного автомобиля? Рекорд скорости для гоночного автомобиля найдите в Интернете.

10. Начертите в тетради возможные графики зависимости координаты от времени для грузовика и легкового автомобиля, если известно, что они ехали в противоположных направлениях, встретились через 1 ч после начала наблюдения, а модуль скорости легкового автомобиля в 3 раза больше, чем модуль скорости грузовика.

11. Зависимость координаты от времени для пешехода выражается формулой x = 30 – 1,5t, а для велосипедиста – формулой x = 15 + 5t. Изобразите на одном чертеже графики зависимости координаты от времени для пешехода и велосипедиста, выбрав такой масштаб, чтобы момент их встречи был отображен на графике. (Здесь и далее числовые значения величин приведены в единицах СИ.)

12. Зависимость координат тела от времени выражается формулами x = 8 – 4t; y = –6 + 3t.
а) Чему равны проекции скорости тела на оси координат?
б) Чему равны проекции перемещения тела за 4 с на оси координат?
в) Изобразите графики зависимости x(t), y(t).
г) Изобразите графики зависимости проекций перемещения от времени.
д) Напишите формулу, выражающую зависимость y(x).
е) Какой путь тело прошло за 4 с?
ж) Изобразите график зависимости пути от времени.

1З. Тело движется прямолинейно и равномерно в координатной плоскости xOy. Проекция скорости тела на ось x равна 60 км/ч. Перемещение тела за 6 мин равно 10 км. Какой может быть проекция скорости тела на ось y?

14. На рисунке 2.7 изображены графики зависимости x(t) для двух тел. Изобразите графики зависимости пути от времени для этих тел.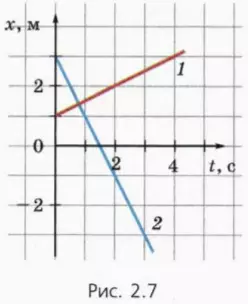

15. Поезд длиной b переезжает через мост длиной d. Скорость поезда равна v.
а) Выразите через b, d, v промежуток времени t₁, в течение которого машинист находился над мостом.
б) Выразите через b, d, v промежуток времени t₂, в течение которого поезд проезжал мимо столба, расположенного при въезде на мост.
в) Выразите через b, d, v промежуток времени t, в течение которого хотя бы часть поезда была на мосту.
г) Найдите длину поезда, если, двигаясь со скоростью 60 км/ч, он ехал по мосту длиной 100 м в течение 30 с.