«Секреты» прямолинейного равноускоренного движения

Продолжим исследование прямолинейного равноускоренного движения, начатое в § 6.

1. Средняя скорость

Напомним (см. § 6), что при прямолинейном движении в одном направлении путь l численно равен площади фигуры, заключенной под графиком зависимости v(t).
Используя этот факт, докажем, что в этом случае средняя скорость равна среднему арифметическому начальной и конечной скорости:

v_ср = (v₀ + v) / 2     (1)

Из определения средней скорости следует, что

l = v_срt.     (2)

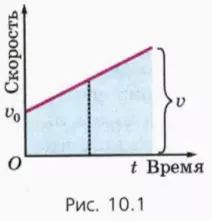
Фигура, заключенная под графиком зависимости v(t), является в данном случае трапецией с основаниями v₀ и v (рис. 10.1). Ее площадь, равную l, можно выразить как произведение средней линии (она показана пунктиром) на высоту. Средняя линия данной трапеции равна полусумме ее оснований v и v₀, а высота равна t. Поэтому получаем:

l = ((v₀ + v) / 2)t.     (3)

Левые части уравнений (2) и (3) одинаковы. Следовательно, их правые части равны, откуда и следует формула (1).

? 1. Начальная скорость автомобиля на участке равна 50 км/ч, а конечная – 70 км/ч. Время движения на участке равно 1 мин. Чему равна длина участка, если автомобиль двигался равноускоренно?

Отметим полезные частные случаи применения формулы для средней скорости равноускоренного движения:

• если v₀ = 0, то v_ср = v/2;
• если v = 0, то v_ср = v₀/2.

Если движение тела не является равноускоренным, то его средняя скорость может быть и не равна среднему арифметическому начальной и конечной скорости!
Рассмотрим примеры.

? 2. На рисунках 10.2 и 10.3 изображены графики зависимости скорости от времени для двух тел. В каком случае средняя скорость меньше среднего арифметического начальной и конечной скорости, а в каком – больше?

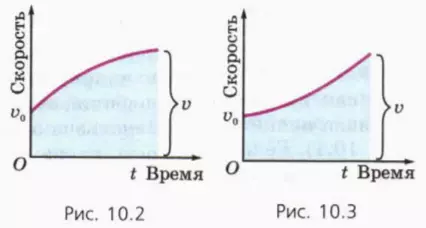
Подсказка. Сравните путь, пройденный каждым из данных тел, с путем, который прошло бы тело, двигавшееся в течение этого же промежутка времени равноускоренно с той же начальной и конечной скоростью.

? 3. Автомобиль разогнался с места до скорости 20 м/с за 10 с, двигаясь равноускоренно. Чему равна средняя скорость автомобиля? Есть ли в условии лишние данные?

? 4. Отойдя от станции, поезд метро разгонялся до некоторой скорости, а потом начал тормозить до остановки на следующей станции. Расстояние между станциями, равное 2 км, поезд проехал за 4 мин. При разгоне и торможении поезд двигался равноускоренно, но с разными по модулю ускорениями.
а) Начертите примерный график зависимости модуля скорости поезда от времени. Какую форму имеет фигура, заключенная под этим графиком?
б) Какова средняя скорость поезда?
в) Какова максимальная скорость поезда?

5. Движущийся прямолинейно равноускоренно автомобиль проехал участок длиной 200 м. Начальная скорость автомобиля равна 10 м/с, а конечная – 30 м/с.
а) Какова средняя скорость автомобиля?
б) За какое время автомобиль проехал участок?

2. Пути, проходимые за последовательно равные промежутки времени

? 6. Галилей доказал, что при прямолинейном равноускоренном движении без начальной скорости пути, проходимые телом за последовательные равные промежутки времени, относятся как последовательные нечетные числа:

l₁ : l₂ : l₃ = 1 : 3 : 5... .

Воспользовавшись рисунком 10.4, докажите это утверждение.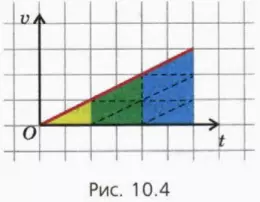

Может быть, кто-то из вас вспомнит, что для свободного падения без начальной скорости такой результат уже был получен (см. задачу 5 из § 7).

А как обобщается эта красивая теорема (теоремой ее назвал сам Галилей) на случай, когда начальная скорость тела не равна нулю?

? 7. Объясните, почему для тела, движущегося прямолинейно равноускоренно в одном направлении, пути, проходимые за последовательные равные промежутки времени продолжительностью τ каждый, образуют арифметическую прогрессию:

l₂ = l₁ + Δ, l₃ = l₂ + 2Δ, ...,

где Δ = aτ² (a – ускорение тела).

Подсказка. Воспользуйтесь рисунком 10.5.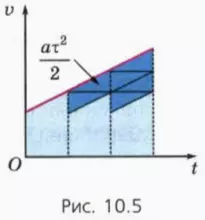

? 8. В первую секунду наблюдения движущийся равноускоренно автомобиль проехал 10 м, а во вторую – 12 м. Наблюдение длилось 5 с. Попробуйте ответить на следующие вопросы устно.
а) Какое расстояние автомобиль проехал за третью, четвертую и пятую секунды?
б) С каким ускорением двигался автомобиль?
в) Чему равна начальная скорость автомобилям?

3. «Последняя секунда»

В некоторых задачах рассматривается заключительный этап движения. Например, дано, что тело за последнюю секунду падения пролетело 30 м или что путь, пройденный падающим телом за последнюю секунду, в n раз больше, чем за предыдущую. Найдем удобный подход к решению подобных задач.

? 9. Пусть тело движется прямолинейно равноускоренно в одном направлении и его скорость увеличивается. Объясните, почему путь, пройденный телом, выражается через его конечную скорость v, ускорение и время движения формулой

l = vt – at²/2.

Подсказка. Воспользуйтесь рисунком 10.6.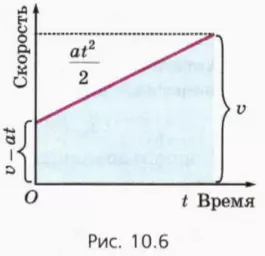

? 10. Свободно падавшее без начальной скорости тело за последнюю секунду падения пролетело 30 м. Попробуйте ответить на следующие вопросы устно.
а) Чему равна скорость тела непосредственно перед ударом о землю?
б) Сколько времени падало тело?

Дополнительные, вопросы и задания

11. Известно, что путь, пройденный за последнюю секунду свободно падающим без начальной скорости телом, в 2 раза больше, чем за предыдущую.
а) Выразите путь, пройденный телом за последнюю секунду, через конечную скорость тела.
б) Выразите путь, пройденный телом за две последние секунду, через конечную скорость тела.
в) Используя условие задачи, напишите соотношение между значениями пути, пройденного за последнюю и предпоследнюю секунды.
г) Найдите конечную скорость тела.
д) Найдите время падения.
е) С какой высоты падало тело?

12. Лыжник съехал с горы длиной l за промежуток времени t, а затем проехал по горизонтальному участку расстояние d до полной остановки. Начальная скорость лыжника равна нулю, движение лыжника на обоих участках можно считать равноускоренным.
а) Чему равна скорость лыжника в конце спуска?
б) Сколько времени длилось торможение?
в) Чему равен модуль ускорения лыжника при движении по горизонтальному участку?

13. Автомобиль движется с постоянным ускорением a. На пути, равном l, скорость автомобиля увеличилась в n раз.
а) Во сколько раз средняя скорость автомобиля на данном участке больше начальной скорости?
б) Чему равна начальная скорость автомобиля?

14. Пути, проходимые за последовательные равные промежутки времени по 1 с телом, которое свободно падает с некоторой начальной скоростью, направленной вниз, относятся, как последовательные натуральные числа:

l₁ : l₂ : l₃ … = 1 : 2 : 3 … .

а) Во сколько раз средняя скорость тела за вторую секунду больше, чем за первую?
б) Насколько средняя скорость тела за вторую секунду больше, чем за первую?
в) Чему равна начальная скорость тела?
г) Начертите график зависимости модуля скорости тела от времени.