Газовые процессы
1. Изобарный процесс (при постоянном давлении)
Экспериментальное изучение газов начнем с процессов, в которых один из трех макропараметров данной массы газа (давление p, объем V или температура T) не изменяется. Такие процессы называют изопроцессами. (От греческого слова «изос» - равный).
Рассмотрим сначала процесс, который происходит при постоянном давлении. Его называют изобарным. (От греческого слова «изос» и «барос» - тяжесть.)
Поставим опыт
Нагревая газ при постоянном давлении (рис. 39.1), мы увидим, что график зависимости объема газа от температуры – отрезок прямой (рис. 39.2).
Если продлить эту прямую в сторону отрицательных значений температуры, то мы заметим, что объем газа должен был бы обратиться в нуль при t = -273 ºС.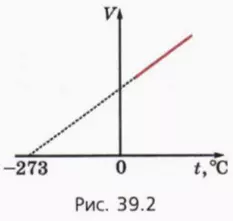
На самом деле объем вещества при t = –273 ºС не становится равным нулю, потому что при охлаждении до очень низких температур газы превращаются сначала в жидкости, а затем – в твердые тела. Поэтому участок графика в области низких температур намечен пунктиром.
Абсолютная шкала температур
В середине 19-го века английский ученый Уильям Томсон предложил шкалу температур, нуль которой соответствует t = –273 ºС. Изменение температуры в один градус по новой шкале ученый предложил сделать равным изменению температуры в один градус по шкале Цельсия.
Эту шкалу температур назвали шкалой Кельвина (такое название обусловлено тем, что У. Томсону за научные заслуги был пожалован титул лорда Кельвина). Ее называют также абсолютной шкалой температур, а температуру, измеренную по этой шкале, – абсолютной температурой. Абсолютную температуру обозначают большой буквой T.
Нуль по абсолютной шкале температур называют абсолютным нулем: это наинизшая температура. Единицу абсолютной температуры называют кельвин (К). Например, температура таяния льда 273 К (говорят: 273 кельвина).
При рассмотрении газовых процессов мы будем использовать далее главным образом абсолютную температуру, не оговаривая этого каждый раз особо.
Соотношение между температурой по шкале Цельсия и абсолютной температурой. Абсолютная температура T и температура t по шкале Цельсия связаны соотношением T = t + 273. На схеме (рис. 39.3) отмечены абсолютный нуль температуры, температура таяния льда и температура кипения воды при атмосферном давлении.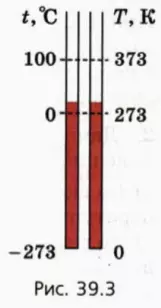
Красный столбик схематически показывает комнатную температуру.
? 1. Какому значению абсолютной температуры соответствуют:
а) комнатная температура (20 ºС);
б) температура кипения воды при атмосферном давлении?
Чтобы изобразить графически зависимость объема газа V от его абсолютной температуры T, достаточно сдвинуть шкалу температур на рисунке 39.2 на 273 градуса влево. В результате получится график, представленный на рисунке 39.4.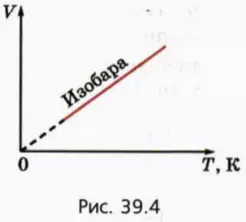
Мы видим, что при постоянном давлении объем данной массы газа прямо пропорционален абсолютной температуре.
Это означает, что
при изобарном процессе отношение объема данной массы газа к его абсолютной температуре остается постоянным:
V/T = const при p = const.
Это соотношение называют законом Гей-Люссака в честь французского ученого, исследовавшего изобарный процесс.
График зависимости V от T при постоянном давлении называют изобарой. Из закона Гей-Люссака следует, что для двух состояний данной массы газа при постоянном давлении
V1/V2 = T1/T2
Например, если абсолютная температура увеличивается в 3 раза, объем газа увеличивается тоже в 3 раза.
При решении задач надо обязательно обращать внимание на то, по какой шкале задана температура газа в условии. Если по шкале Цельсия, то первое, что надо сделать, – выразить все значения температуры по абсолютной шкале.
? 2. Данная масса газа расширяется изобарно. Начальная и конечная температуры газа 20 ºС и 200 ºС.
а) Во сколько раз увеличилось значение абсолютной температуры газа?
б) Во сколько раз увеличился объем газа?
в) Изобразите график зависимости V(T) для данного процесса.
? 3. Объясните, почему графики, изображенные на рисунке 39.5, являются графиками одного и того же изобарного процесса с данной массой газа в координатах (V, T), (p, T) и (p, V).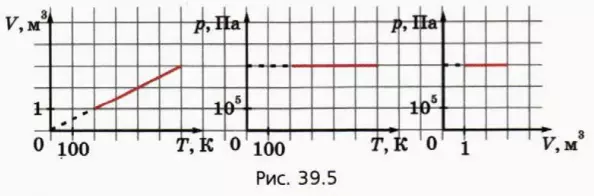
? 4. Изобразите графики процесса, описанного в задании 2, в координатах (p, T) и (p, V).
2. Изохорный процесс (при постоянном объеме)
Процесс, происходящий с данной массой газа при постоянном объеме, называют изохорным. (От греческих слов «изос» и «хорема» - сосуд.)
Поставим опыт
Сосуд с некоторой массой воздуха соединим с манометром и поместим в сосуд с водой (рис. 39.6). Объем сосуда остается постоянным.
Нагревая воду, будем увеличивать температуру газа.
Измеряя зависимость давления газа от абсолютной температуры, мы обнаружим, что при постоянном объеме давление данной массы газа прямо пропорционально абсолютной температуре.
Это означает, что
при изохорном процессе отношение давления данной массы газа к его абсолютной температуре остается постоянным:
p/T = const при V = const.
Это соотношение называют законом Шарля в честь французского ученого, который установил его на опыте.
График зависимости p от T при постоянном объеме называют изохорой (рис. 39.7). Он показывает, что при постоянном объеме давление газа прямо пропорционально его абсолютной температуре.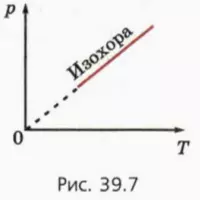
Из закона Шарля следует, что для двух состояний данной массы газа при постоянном объеме выполняется соотношение
p1/p2 = T1/T2
Например, если абсолютная температура газа увеличилась в 2 раза, то давление газа увеличилось тоже в 2 раза.
? 5. Изобразите графики изохорного процесса в координатах (V, T) и (p, V).
? 6. Начальная и конечная температуры данной массы газа в изохорном процессе равны соответственно 327 ºС и 27 ºС.
а) Во сколько раз уменьшилась абсолютная температура газа?
б) Во сколько раз уменьшилось давление газа?
в) Изобразите графики зависимости p(T), V(T) и p(V) для данного процесса.
? 7. На рисунке 39.8, а изображен график зависимости p(T) для процесса, происходящего с некоторой массой газа. Процесс проводили в два этапа.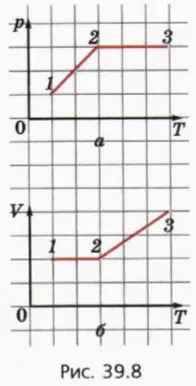
а) Объясните, почему график зависимости V(T) на рисунке 39.8, б соответствует тому же процессу.
б) Каким изопроцессом является процесс 1–2? Во сколько раз увеличилось давление газа в этом процессе?
в) Каким изопроцессом является процесс 2–3? Во сколько раз увеличился объем газа в этом процессе?
г) Во сколько раз надо уменьшить температуру газа при постоянном объеме, чтобы при переходе из состояния 3 в состояние 4 (не изображенное на рисунке 39.8) давление газа стало таким же, как в состоянии 1? Перенесите графики в тетрадь и укажите на них состояние 4.
? 8. Объем данной массы газа увеличили в 2 раза при постоянном давлении, а затем давление газа уменьшили в 3 раза при постоянном объеме.
а) Как изменилась температура газа в первом процессе?
б) Как изменилась температура газа во втором процессе?
в) Чему равно отношение конечной температуры газа к начальной?
г) Изобразите графики описанного процесса в координатах (V, T), (p, V) и (p, T).
3. Изотермический процесс (при постоянной температуре)
Процесс, происходящий с данной массой газа при постоянной температуре, называют изотермическим.
Поставим опыт
Сосуд с некоторой массой газа соединим с манометром. Объем сосуда можно изменять (рис. 39.9).
Если изменять объем газа медленно, то вследствие теплообмена с воздухом температура газа в сосуде остается все время постоянной (равной температуре воздуха).
Изучая зависимость давления газа от его объема при постоянной температуре, мы обнаружим, что
при изотермическом процессе произведение давления данной массы газа на его объем остается постоянным:
pV = const при T = const.
Это соотношение было установлено на опыте во второй половине 17-го века р английским ученым Бойлем и французским ученым Мариоттом, поэтому его называют законом Бойля–Мариотта.
? 9. Объясните, почему закон Бойля–Мариотта можно сформулировать так: при постоянной температуре давление данной массы газа обратно пропорционально его объему.
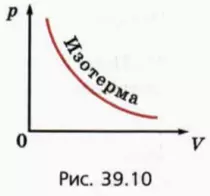
График зависимости давления данной массы газа от объема при постоянной температуре называют изотермой (рис. 39.10). Это – гипербола. Из закона Бойля–Мариотта следует, что для двух состояний данной массы газа при постоянной температуре
p1/p2 = V2/V1
Например, если объем газа в 3 раза увеличился, то давление газа уменьшилось в 3 раза.
? 10. Изобразите графики изотермического процесса в координатах (p, T) и (V, T).
? 11. При изотермическом расширении объем данной массы газа увеличился в 2 раза.
а) Как изменилось давление газа?
б) Насколько уменьшилось давление газа, если начальное давление равно 105 Па?
4. Уравнение Клапейрона
Рассмотрим теперь процессы с данной массой газа, при которых одновременно изменяются все три параметра – давление p, объем V и температура T.
В первой половине 19-го века французский физик Бенуа Клапейрон вывел одно соотношение, которое связывает эти три параметра: для данной массы газа произведение давления газа на его объем, деленное на абсолютную температуру газа, есть величина постоянная:
pV/T = const.
Это соотношение называют уравнением Клапейрона.
? 12. Покажите, что уравнения трех изопроцессов являются частными случаями уравнения Клапейрона.
Сравнение двух изохор, двух изобар и двух изотерм
Воспользуйтесь уравнением Клапейрона при выполнении следующего задания.
? 13. На рисунке 39.11 изображены две изохоры, две изобары и две изотермы для одной и той же массы газа.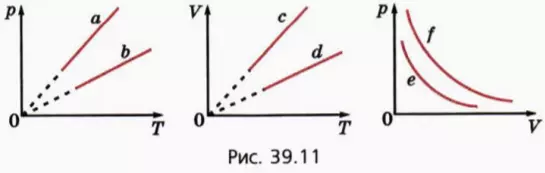
а) Какой изохоре соответствует больший объем?
б) Какой изобаре соответствует большее давление?
в) Какой изотерме соответствует большая температура?
? 14. Когда сосуд с данной массой газа перенесли из смеси воды со льдом в кипяток, объем газа увеличился в 1,5 раза.
а) Чему равны начальная и конечная абсолютные температуры газа?
б) Чему равно отношение конечного и начального давлений газа?
Подсказка. Воспользуйтесь уравнением Клапейрона.

Дополнительные вопросы и задания
16. Начальная температура данной массы газа равна 0 ºС. Давление газа постоянно.
а) Какова конечная абсолютная температура газа, если его объем увеличился в 2 раза? в 3 раза?
б) Изобразите графики зависимости V(T), p(T) и p(V) для данного процесса.
16. Начальная температура данной массы газа равна 0 ºС. Объем газа постоянен.
а) Какова конечная абсолютная температура газа, если его -„.:: давление уменьшилось в 2 раза? в 3 раза?
б) Изобразите графики зависимости V(T), p(T) и p(V) для данного процесса.
17. В начальном состоянии параметры данной массы газа равны p0, V0, T0. С газом осуществляют процесс, состоящий из трех последовательных этапов:
1) изобарное расширение, при котором объем газа увеличился в 2 раза;
2) изохорное охлаждение, при котором давление газа уменьшилось в 4 раза;
3) изотермическое сжатие, при котором объем газа уменьшился в 3 раза.
Чему равны p, V и T по окончании:
а) первого этапа;
б) второго этапа;
в) третьего этапа?
Изобразите в координатах (V; T), (p, T) и (p, V) графики газового процесса, состоящего из трех этапов.
18. На рисунке 39.12 приведен график циклического процесса для данной массы газа. В результате циклического процесса газ возвращается в начальное состояние.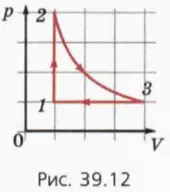
а) Во сколько раз изменяются давление, объем и температура газа на каждом из трех этапов процесса?
б) Изобразите графики этого же циклического процесса в координатах (V; T) и (p, T).
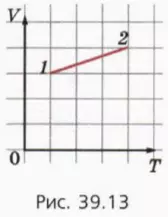
19. На рисунке 39.13 изображен график процесса, происходящего с некоторой массой газа. Как изменилось давление , газа в результате процесса?
Подсказка. Воспользуйтесь уравнением Клапейрона.