Закон Архимеда. Плавание тел

Вы уже знаете, что внутри жидкости в любой точке существует гидростатическое давление. Поэтому если внутрь жидкости в сосуде поместить тело (например, шар), то на все точки его поверхности будут действовать силы гидростатического давления (рис. 165, а). Определим сумму этих сил.

Для этого рассмотрим второй такой же сосуд, заполненный, как и первый, такой же жидкостью (рис. 165, б). Выделим мысленно во втором сосуде объем жидкости, границы которого совпадают с границами тела в первом сосуде. Поскольку этот объем жидкости покоятся относительно Земли, то сумма всех действующих на него сил равна нулю. Иначе говоря, сумма сил гидростатического давления, действующих на выделенный объем жидкости, уравновешивает действующую на него силу тяжести. Следовательно, сумма сил гидростатического давления равна по модулю силе тяжести выделенного объема жидкости. Эта сумма сил направлена вертикально вверх (рис. 165, в). Поэтому ее называют выталкивающей силой.

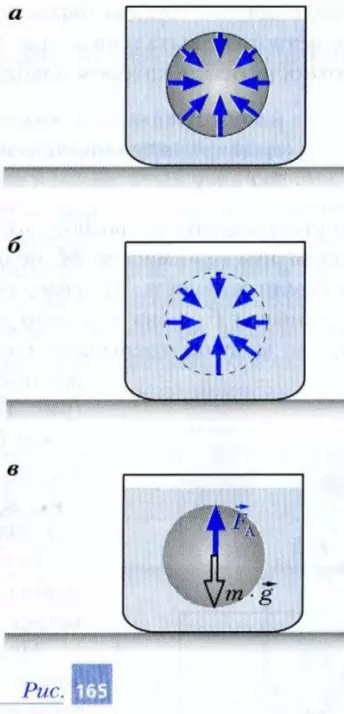
Сумма сил гидростатического давления, действующих на выделенный объем покоящейся жидкости в сосуде, равна по модулю весу выделенного объема жидкости и направлена вертикально вверх.

Понятно, что на тело в первом сосуде со стороны окружающей жидкости действует такая же выталкивающая сила. Впервые на существование этой силы указал древнегреческий ученый Архимед. Поэтому выталкивающую силу F_A обычно называют силой Архимеда.

Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.

Поскольку масса m выделенного объема жидкости равна произведению ее плотности ρ_ж и объема V, то модуль силы Архимеда F_A = ρ_ж · g · V. Другими словами, сила Архимеда по модулю равна весу вытесненной телом жидкости.

Если тело поместить в газ, то на это покоящееся тело будут действовать силы давления со стороны окружающего газа. Поэтому на такое тело также будет действовать выталкивающая сила, равная по модулю F_A = ρ_г · g · V, где ρ_г – плотность газа, в котором находится тело, V – объем тела. Таким образом,

на погруженное в жидкость (или газ) тело действует выталкивающая и направленная вертикально вверх сила, равная по модулю весу вытесненной этим телом жидкости (или газа).

Это утверждение называют законом Архимеда.

Рассмотрим тело массой M, целиком погруженное в покоящуюся относительно Земли жидкость. Помимо суммы сил гидростатического давления – силы Архимеда F_A – на это тело действует сила тяжести Mg. Если сила тяжести по модулю превышает силу Архимеда, то это тело будет все глубже погружаться в жидкость, т. е. будет тонуть (рис. 166, а). Так как модуль силы тяжести Mg равен (ρ_т · V) · g, где ρ_т – средняя плотность теаа, то тело будет тонуть, если (ρ_т · V) · g > ρ_ж · g · V, т. е. если средняя плотность тела будет больше плотности жидкости: ρ_т > ρ_ж.

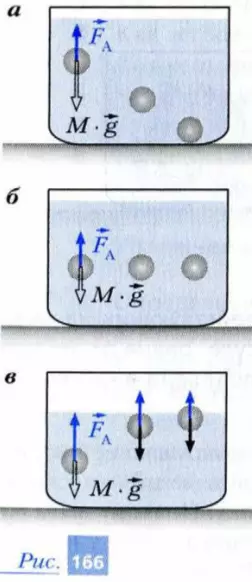
Если же модули сил тяжести и Архимеда равны (при этом ρ_т = ρ_ж), то тело будет оставаться в покое (рис. 166, б).

Наконец, если сила тяжести по модулю окажется меньше силы Архимеда (когда ρ_тж), то тело будет всплывать (рис. 166, в). После того как тело своей верхней границей достигнет поверхности жидкости и будет продолжать подниматься, все более выступая над поверхностью, объем погруженной в жидкости части тела будет уменьшаться. Поэтому выталкивающая сила со стороны жидкости также начнет уменьшаться, пока не станет равной по модулю силе тяжести:

F_в = Mg

Для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой.

Это равенство является условием плавания тела на поверхности жидкости. Модуль выталкивающей силы F_в = ρ_ж · g · V_ж, где V_ж – объем вытесненной телом жидкости. Поэтому условие плавания тела на поверхности жидкости F_т = F_в можно представить в виде:

ρ_т · V_т = ρ_ж · V_ж

Рассмотрим примеры применения закона Архимеда для решения практических задач.

Задача 1. Определение подъемной силы воздушного шара

Воздушные шары используют в воздухоплавании для подъема грузов (людей, приборов и т. п.). Для того чтобы шар с грузом мог взлететь, его наполняют газом, плотность которого меньше плотности окружающего воздуха. Таким газом может быть, например, гелий. Однако в последнее время чаще используют нагретый воздух, так как плотность воздуха уменьшается при нагревании. Для нагревания воздуха внутри воздушного шара снизу в нем делают отверстие, под которым располагают горелку. Нагревание воздуха внутри шара и уменьшение его плотности приводит к появлению подъемной силы.

Подъемной силой шара называют силу, равную по модулю весу груза, г которым шар может подниматься равномерно: F_под = P. Определите эту силу.

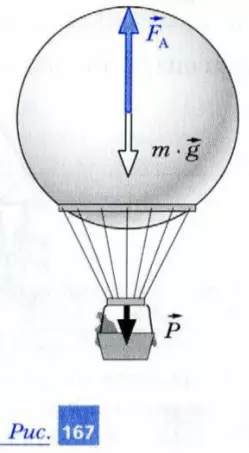
Решение. На рис. 167 изображены воздушный шар и действующие на него силы: сила тяжести mg, сила Архимеда F_A и P – вес груза. Если шар поднимается равномерно, то его ускорение равно нулю. Поэтому по второму закону Ньютона:

F_A - m · g - P = m · a = m · 0 = 0.

Следовательно,

P = F_A - m · g.

Поэтому

F_под = P = F_A - m · g.

Подъемная сила воздушного шара равна разности модулей действующих на этот шар силы Архимеда и силы тяжести.

Задача 2. Определение водоизмещения и грузоподъемности судна

Пусть судно массой M стоит у причала под погрузкой (рис. 168). На судно помещен груз массой m и судно находится в равновесии. Определите объем той части судна, которая находится ниже уровня воды.

Решение. По второму закону Ньютона сумма сил, действующих на судно, равна нулю (условие плавания):

F_A - (m + M) · g = 0

Вместе с тем модуль силы Архимеда F_A = ρ_в · g · V_п. Здесь ρ_в – плотность воды, а V_п – объем той части судна, которая находится ниже уровня воды. Подставляя выражение для FA в условие плавания, получаем:

ρ_в · g · V_п - (m + M) · g = 0

Следовательно,

V_п = (m + M) / ρ_в

Из последнего выражения видно, что чем больше масса m груза, тем большая часть судна V_п погружается под воду. С увеличением массы груза увеличивается осадка судна – глубина, на которую судно погружается в воду. Максимально допускаемую при загрузке осадку отмечают на корпусе судна линией. Ее называют ватерлинией.

Модуль веса воды, вытесняемой судном при погружении до ватерлинии, называют водоизмещением судна.

Обозначим объем той части судна, которая находится ниже ватерлинии, V_max. Тогда водоизмещение судна равно ρ_в · g · V_max.

Подставляя это выражение в условие плавания, легко найти модуль силы тяжести, действующей на груз максимально допустимой массы:

ρ_в · g · V_max - (m_max + M) · g = 0,
m_max · g = ρ_в · g · V_max - M · g.

Полученную величину называют грузоподъемностью судна. Видно, что грузоподъемность судна равна разности его водоизмещения и модуля силы тяжести судна без груза.

Итоги

Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.

Закон Архимеда. На погруженное в жидкость (или газ) тело действует выталкивающая и направленная вертикально вверх сила, равная по модулю весу вытесненной этим телом жидкости (или газа).

F_A = ρ_ж · g · V

Тело тонет, если ρ_т > ρ_ж; тело всплывает, если ρ_тж.

Условие плавания тела на поверхности жидкости:
для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой:

F_в = M · g

Условие плавания тела на поверхности жидкости можно представить в виде

ρ_т · V_т = ρ_ж · V_ж

Вопросы

1. Какие силы действуют на любое тело, находящееся внутри жидкости или газа?
2. Сформулируйте закон Архимеда.
3. В каком случае тело тонет в жидкости, а в каком всплывает?
4. Почему, находясь под водой, человек может поднять предмет, который он, находясь на суше, не может даже сдвинуть с места?
5. Почему гусиное яйцо тонет в пресной воде, а в соленой плавает?
6. Как зависит глубина погружения плавающего на поверхности жидкости тела от его плотности?
7. Куда направлена сумма сил гидростатического давления, действующих на кубик, который прилип к горизонтальному дну озера своей нижней гранью?
8. К чашкам равноплечих весов подвешены два шарика одинаковой массы. Нарушится ли равновесие весов при погружении шариков в воду, если: а) оба шарика медные; б) один шарик железный, а другой – медный?
9. К чашкам равноплечих весов подвешены два одинаковых стальных шарика. Нарушится ли равновесие весов при погружении шариков в разные жидкости, плотности которых: а) равны; б) различаются в два раза?

Упражнения

1. Пользуясь таблицей плотностей, укажите, шарики из каких металлов будут плавать в ртути, а из каких – тонуть.
2. Пользуясь таблицей плотностей, рассчитайте, какая часть однородной льдины выступает над поверхностью воды в озере.
3. Пользуясь таблицей плотностей, рассчитайте, какая часть однородного березового куба, плавающего на поверхности воды, будет погружена в воду.
4. Определите подъемную силу детского воздушного шарика, заполненного гелием. Объем шарика V = 5 дм³. Масса его оболочки m = 5 г. Плотность гелия считайте равной ρ_г = 0,19 кг/м³, а плотность воздуха атмосферы ρв = 1,3 кг/м³.
5. После разгрузки баржа поднялась из воды на 1 м. Определите вес снятого с баржи груза, считая площадь сечения баржи на уровне воды постоянной и равной 350 м².
6. После погрузки на паром длиной 40 м и шириной 10 м двух одинаковых комбайнов он погрузился в воду на 10 см. Найдите массу комбайна.