Сообщающиеся сосуды
На рис. 156 изображено несколько сосудов, соединенных снизу между собой трубкой. Такие сосуды называют сообщающимися. Если в сообщающиеся сосуды налить однородную жидкость, то эксперимент показывает, что поверхности жидкости во всех сосудах установятся на одной высоте h.
В сообщающихся сосудах поверхности однородной жидкости устанавливаются на одном уровне.
Это явление можно объяснить, используя выведенную формулу для расчета гидростатического давления. Поскольку жидкость находится в состоянии покоя, то ее давление в точках A, B, C и D, находящихся на одном горизонтальном уровне, должно быть одинаковым. В противном случае жидкость, находящаяся между этими точками, начала бы двигаться. Давление в рассматриваемых точках определяется атмосферным давлением, плотностью жидкости и высотой ее столба. Так как налитая жидкость однородна и атмосферное давление на поверхности жидкости во всех сосудах одинаково, то высота столбов жидкости во всех сосудах должна быть одинакова.
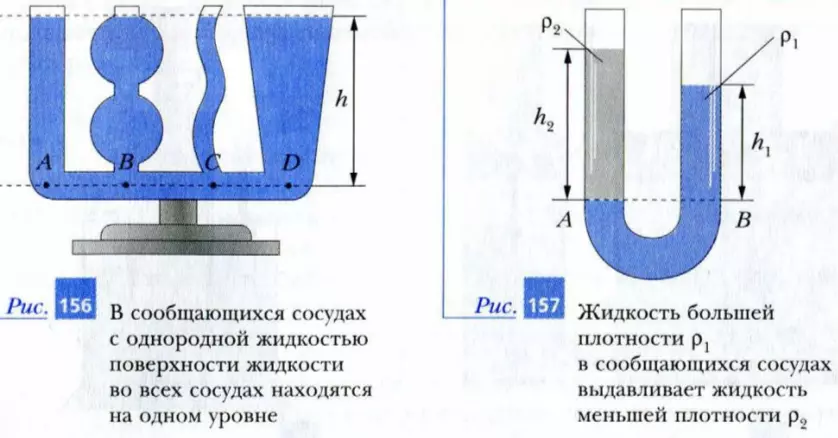
Наоборот, если в сообщающиеся сосуды налить разные по плотности жидкости, то высота столбов этих жидкостей будет разной. На рис. 157 изображена U-образная трубка, в правое колено которой налили жидкость с плотностью ρ1, а в левое колено – жидкость с плотностью ρ2. В данном случае ρ1 > ρ2. Поэтому более плотная жидкость выдавливает менее плотную и частично заполняет левое колено. Так как жидкости покоятся, то гидростатические давления в правом и левом коленах на уровне AB границы раздела жидкостей равны. Из формулы для расчета гидростатического давления находим
pA = pатм + ρ2 · g · h2 и pB = pатм + ρ1 · g · h1.
Поэтому ρ2 · g · h2 = ρ1 · g · h1, или ρ2 · h2 = ρ1 · h1.
Проанализируем полученное соотношение. Если ρ1 > ρ2 в некоторое число раз, то h12 в такое же число раз.
Разновидности сообщающихся сосудов находят широкое применение в науке и технике. Рассмотрим один из примеров — гидравлический пресс.
Принцип работы гидравлического пресса иллюстрирует устройство, показанное на рис. 158. Оно состоит из двух сообщающихся цилиндров разных диаметров, в которых могут без трения двигаться легкие поршни. Обозначим площадь меньшего поршня S1, а большего – S2. Цилиндры заполнены жидкостью, предназначенной для передачи гидростатического давления.

Если приложить к меньшему поршню силу F1 (например, поставить на него груз), то эта сила создаст в жидкости добавочное давление p1 = F1/S1. Для того чтобы устройство осталось в равновесии, ко второму поршню нужно приложить силу F2, которая создаст в жидкости давление p2 = F2/S2, равное p1. Следовательно, F2/S2 = F1/S1. Или, по-другому, F2/F1 = S2/S1. То есть F2 во столько раз больше F1, во сколько раз площадь большего поршня S2 больше площади поршня S1. Таким образом, с помощью гидравлического пресса можно получить выигрыш в силе, равный S2/S1. Иначе говоря, прикладывая к малому поршню небольшую силу, можно большим поршнем создать очень большое усилие.
В настоящее время гидравлические прессы способны развивать силу 108 Н. Они используются для штамповки деталей из листового металла, выдавливания профилей, а также для прессования различных материалов – фанеры, картона и др.
По этому же принципу работают гидравлические домкраты (рис. 159), гидравлические усилители автомобильных тормозов и гидравлические усилители руля.
Итоги
Сосуды, соединенные снизу между собой трубкой, называют сообщающимися сосудами.
В сообщающихся сосудах поверхности однородной жидкости устанавливаются на одном уровне.
Если сообщающиеся сосуды заполнены жидкостями разной плотности, то высоты столбов жидкостей над уровнем границы их раздела определяются соотношением: ρ2 · h2 = ρ1 · h1.
В гидравлическом прессе сообщающиеся сосуды разных сечений S2 и S1, заполненные однородной жидкостью, используют для получения выигрыша в силе F2/F1, равного S2/S1.
Вопросы
- Какие сосуды называют сообщающимися? Приведите примеры сообщающихся сосудов.
- От чего зависит разность уровней жидкости в сообщающихся сосудах?
- Что такое гидравлический пресс? Приведите примеры устройств, работающих по тому же принципу, что и гидравлический пресс.
- Каким образом с помощью гидравлического пресса можно получить выигрыш в силе? Можно ли с помощью гидравлического пресса получить выигрыш в работе?
Упражнения
- Найдите, во сколько раз различаются высоты столбов жидкостей над уровнем границы их раздела в сообщающихся сосудах, если плотности жидкостей различаются в два раза (см. рис. 157).
- Как с помощью сообщающихся сосудов и воды определить плотность масла? Плотность воды считать известной.
- Какой максимальный выигрыш в силе можно получить с помощью гидравлического пресса, площади поршней которого S1 = 4 см2 и S2 = 2 м2? Чему будет равен в этом случае модуль силы, действующей на большой поршень, при действии на малый поршень силы, модуль которой равен 600 Н?
- На сколько нужно переместить малый поршень пресса из упражнения 3, чтобы большой поршень переместился на 1 мм?
- Под действием силы 100 Н малый поршень гидравлического пресса опустился на 20 см. При этом большой поршень поднялся на 5 см. Какая максимальная сила гидростатического давления действовала на большой поршень?
