Ускорение
В курсе физики VII класса вы изучали самый простой вид движения — равномерное движение по прямой линии. При таком движении скорость тела была постоянной и тело за любые равные промежутки времени проходило одинаковые пути.
Большинство движений, однако, нельзя считать равномерными. На одних участках тела могут иметь меньшую скорость, на других — большую. Например, поезд, отходящий от станции, начинает двигаться все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.
Проделаем опыт. Установим на тележку капельницу, из которой через одинаковые промежутки времени падают капли окрашенной жидкости. Поместим эту тележку на наклонную доску и отпустим. Мы увидим, что расстояние между следами, оставленными каплями, по мере движения тележки вниз будет становиться все больше и больше (рис. 3). Это означает, что за равные промежутки времени тележка проходит неодинаковые пути. Скорость тележки возрастает. Причем, как можно доказать, за одни и те же промежутки времени скорость тележки, съезжающей по наклонной доске, возрастает все время на одну и ту же величину.
Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным.
Так, например, опытами установлено, что скорость любого свободно падающего тела (при отсутствии сопротивления воздуха) за каждую секунду возрастает примерно на 9,8 м/с, т. е. если вначале тело покоилось, то через секунду после начала падения оно будет иметь скорость 9,8 м/с, еще через секунду — 19,6 м/с, еще через секунду — 29,4 м/с и т. д.
Физическая величина, показывающая, на сколько изменяется скорость тела за каждую секунду равноускоренного движения, называется ускорением.
a — ускорение.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Ускорение характеризует быстроту изменения скорости. Если, например, ускорение тела равно 10 м/с2, то это означает, что за каждую секунду скорость тела изменяется на 10 м/с, т. е. в 10 раз быстрее, чем при ускорении 1 м/с2.
Примеры ускорений, встречающихся в нашей жизни, можно найти в таблице 1.
Как рассчитывают ускорение, с которым тела начинают двигаться?
Пусть, например, известно, что скорость отъезжающего от станции электропоезда за 2 с увеличивается на 1,2 м/с. Тогда, для того чтобы узнать, на сколько она возрастает за 1 с, надо 1,2 м/с разделить на 2 с. Мы получим 0,6 м/с2. Это и есть ускорение поезда.
Итак, чтобы найти ускорение тела, начинающего равноускоренное движение, надо приобретенную телом скорость разделить на время, за которое была достигнута эта скорость: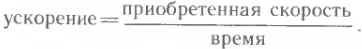
Обозначим все величины, входящие в это выражение, латинскими буквами:
a — ускорение; v — приобретенная скорость; t — время.
Тогда формулу для определения ускорения можно записать в следующем виде: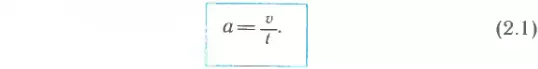
Эта формула справедлива для равноускоренного движения из состояния покоя, т. е. когда начальная скорость тела равна нулю. Начальную скорость тела обозначают Формула (2.1), таким образом, справедлива лить при условии, что v0 = 0.
Если же нулю равна не начальная, а конечная скорость (которая обозначается просто буквой v), то формула ускорения принимает вид:
В таком виде формулу ускорения применяют в тех случаях, когда тело, имеющее некоторую скорость v0, начинает двигаться все медленнее и медленнее, пока наконец не остановится (v = 0). Именно по этой формуле, например, мы будем рассчитывать ускорение при торможении автомобилей и других транспортных средств. Под временем t при этом мы будем понимать время торможения.
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость (рис. 4, а); если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону (рис. 4, б).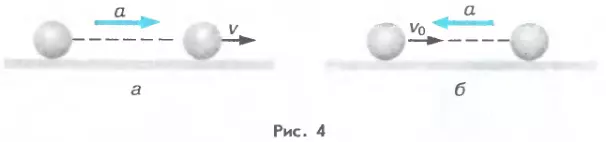
При равномерном прямолинейном движении скорость тела не изменяется. Поэтому ускорение при таком движении отсутствует (a = 0) и на рисунках изображено быть не может.
1. Какое движение называют равноускоренным? 2. Что такое ускорение? 3. Что характеризует ускорение? 4. В каких случаях ускорение равно нулю? 5. По какой формуле находится ускорение тела при равноускоренном движении из состояния покоя? 6. По какой формуле находится ускорение тела при уменьшении скорости движения до нуля? 7. Как направлено ускорение при равноускоренном прямолинейном движении?
Экспериментальное задание. Используя линейку в качестве наклонной плоскости, положите на ее верхний край монету и отпустите. Будет ли двигаться монета? Если будет, то как — равномерно или равноускоренно? Как это зависит от угла наклона линейки?
