Механическая энергия системы тел. Закон сохранения механической энергии

Мы изучали различные виды энергии, которыми обладают тела или системы тел. При этом было установлено, что кинетическая энергия определяется движением тел и их массой и зависит от механических параметров системы (масс тел и их скоростей). Потенциальная энергия системы тел определяется их взаимодействием и также зависит от механических параметров (взаимного положения, т. е. координат тел системы, их масс и т. д.). Таким образом, эти виды энергии – кинетическая и потенциальная – определяются механическим состоянием системы тел. Их сумму называют механической энергией системы тел.

Сумму потенциальной и кинетической энергий называют механической энергией системы тел.

В дальнейшем механическую энергию системы тел мы будем обозначать буквой Е.

Е = К + П

Рассмотрим, как изменяются кинетическая и потенциальная энергии системы тел на примере свободного падения тела в системе «тело – Земля». При падении тела вниз под действием силы тяжести скорость тела увеличивается. Следовательно, его кинетическая энергия нарастает. При этом расстояние от тела до поверхности Земли уменьшается. Значит, потенциальная энергия системы тел уменьшается при одновременном увеличении кинетической энергии.

При подъеме тела, напротив, потенциальная энергия системы возрастает. Скорость тела при этом уменьшается. Следовательно, кинетическая энергия системы уменьшается при одновременном увеличении потенциальной энергии.

Отметим, что в рассмотренных примерах силы трения в системе считают пренебрежимо малыми (при свободном падении тело движется только пол действием силы тяжести). Поэтому работа сил трения в системе равна нулю. Также пренебрежимо малыми считают внешние силы (силы, действующие на тело и Землю со стороны тел, не входящих в систему). Поэтому их работа также равна нулю.

Можно показать, и многочисленные эксперименты это подтверждают, что если суммарная работа внутренних сил трения и внешних сил равна нулю, то механическая энергия системы тел – сумма потенциальной и кинетической энергий системы – не изменяется.

Механическая энергия системы тел в инерциальной системе отсчета не изменяется, если суммарная работа внутренних сил трения и внешних сил равна нулю.

П₀ + К₀ = П_к + К_к,
если А_тр + А_ex = 0.

Написанное соотношение вместе с условием называют законом сохранения механической энергии.

Для того чтобы усвоить смысл этого закона и научиться правильно его использовать, рассмотрим решение нескольких задач.

Задача 1. «Падение»

Определите модуль vк скорости, с которой подлетит к поверхности Земли камень, начавший свободно падать без начальной скорости (v₀ = 0) с высоты h₀ = 20 м. Модуль ускорения свободного падения считайте равным g = 10 м/с².

Решение. Будем решать задачу в системе отсчета, связанной с Землей, ось X направим вертикально вверх. Рассмотрим систему «камень – Земля». В начальный момент потенциальная энергия этой системы тел равна П₀ = m · g · h₀, где m – масса камня. Начальная кинетическая энергия системы К₀ = 0. (Объясните почему.) При падении камня его кинетическая энергия будет нарастать. При этом потенциальная энерния рассматриваемой системы тел будет уменьшаться. В момент подлета к Земле h_к = 0. Поэтому П_к = m · g · h_к = 0. Кинетическая энергия системы в этот момент будет равна кинетической энергии камня, т. е. К_к = (m · v_к²) / 2. Сил сопротивления движению камня нет – он совершает свободное падение. Нет и внешних сил – взаимодействие камня и Земли с другими объектами мы не учитываем. Следовательно, работа внешних сил и сил трения равна нулю. Воспользуемся законом сохранения механической энергии:

П₀ + К₀ = П_к + К_к.

Подставим в это соотношение найденные значения энергий системы:

m · g · h₀ + (m · v₀²) / 2 = m · g · h_к + (m · v_к²) / 2 ,
m · g · h₀ + 0 = 0 + (m · v_к²) / 2 ,
v_к² = 2g · h₀ = 20 · 20 (м²/с²).

Следовательно, v_к = 20 м/с.

Ответ: модуль скорости, с которой камень подлетит к поверхности Земли, равен 20 м/с.

Отметим, что в рассмотренной задаче потенциальная энергия системы тел полностью перешла в кинетическую энергию.

Задача 2. «Подъем»

Определите максимальную высоту h_к, на которую поднимется камень, если его скорость у поверхности Земли направлена вертикально вверх, а ее модуль v₀ = 30 м/с. Модуль ускорения свободного падения считайте равным g = 10 м/с².

Решение. Выберем систему отсчета, связанную с Землей, ось X направим вертикально вверх. В качестве системы тел, как и прежде, рассмотрим камень и Землю. Будем считать, что сил сопротивления движению камня нет – он движется, испытывая действие только внутренней потенциальной силы (силы тяжести). Следовательно, камень, поднимаясь вверх, совершает свободное падение.

Начальная потенциальная энергия рассматриваемой системы тел равна

П₀ = m · g · h₀ = m · g · 0 = 0,

а ее начальная кинетическая энергия –

К₀ = (m · v₀²) / 2 .

В момент достижения камнем максимальной высоты hк его скорость станет равна нулю (v_к = 0). Поэтому кинетическая энергия системы тел будет равна

К_к = (m · v_к²) / 2 = ½ m · 0 = 0.

Потенциальная энергия системы будет равна П_к = m · g · hк, где h_к – искомая максимальная высота, на которую поднимется камень. Подставим полученные значения начальных и конечных потенциальных и кинетических энергий системы в закон сохранения механической энергии П₀ + К₀ = П_к + К_к. Получим:

0 + (m · v₀²) / 2 = m · g · h_к + 0.

Следовательно,

h_к = v₀² / 2g = (30 м/с)² / (2 · 10 м/с²) = 900/20 м = 45 м.

Ответ: максимальная высота, на которую поднимется камень, равна h_к = 45 м.
Отметим, что в процессе подъема начальная кинетическая энергия камня полностью перешла в потенциальную энергию системы «камень – Земля». При этом потенциальная энергия системы возросла на величину, в точности равную убыли кинетической энергии.

Из рассмотренных примеров можно сделать важный вывод.

При свободном падении камня (этапы «подъем» и «падение») изменение потенциальной энергии системы «камень – Земля» равно изменению кинетической энергии этой системы, взятому с обратным знаком.

Задача 3. «Сжатие пружины»

На легкую упругую пружину жесткостью k = 1 МН/м, прикрепленную к стене, налетает скользящий по гладкой горизонтальной плоскости брусок массой m = 25 кг (рис. 134). Модуль скорости бруска v = 10 м/с. Определите максимальное сжатие пружины под действием этого бруска.

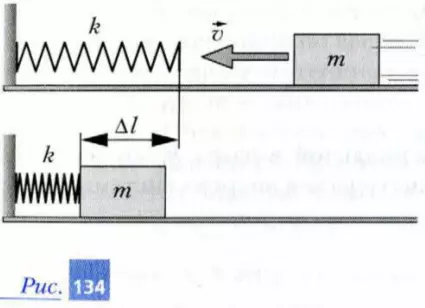
Решение. Будем решать задачу в системе отсчета, связанной с Землей. Рассмотрим систему тел, состоящую из пружины и бруска. В момент касания бруском пружины кинетическая энергия системы тел равна К₀ = (m · v²) / 2. При этом потенциальная энергия нашей системы равна нулю, так как пружина не деформирована. Работа внешних сил (силы тяжести и реакций опор) равна нулю. Сил трения нет. К моменту максимального сжатия пружины на величину Δl брусок остановится. Следовательно, конечная кинетическая энергия указанной системы тел будет равна нулю. При этом потенциальная энергия системы станет равной П_к = (k · Δl²) / 2. Воспользуемся законом сохранения механической энергии П₀ + К₀ = П_к + К_к. Подставим в это соотношение найденные значения энергий:

0 + (m · v²) / 2 = (k · Δl²) / 2 + 0.

Следовательно,

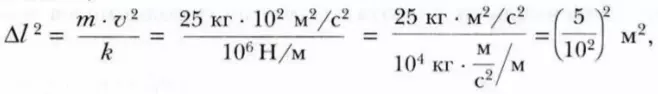
Δl = 5 / 100 (м) = 5 см.

Ответ: пружина сожмется на 5 см.

Обратим внимание на то, что мы не смогли бы решить эту задачу, используя непосредственно законы Ньютона и определение работы. Это связано с тем, что совершающая работу сила упругости не остается постоянной – эта сила изменяется при сжатии пружины.

Итоги

Сумму потенциальной и кинетической энергий называют механической энергией системы тел.

Е = К + П

Закон сохранения механической энергии.

Механическая энергия системы тел в инерциальной системе отсчета не изменяется, если суммарная работа внутренних сил трения и внешних сил равна нулю.

П₀ + К₀ = П_к + К_к,
если А_тр + А_ex = 0.

При подъеме тела с поверхности Земли и действии на него только силы тяжести кинетическая энергия системы «тело – Земля» переходит в потенциальную; при свободном падении тела с высоты потенциальная энергия системы «тело – Земля» переходит в кинетическую.

Использование закона сохранения механической энергии позволяет упростить решение многих задач.

Вопросы

1. Что такое механическая энергия системы тел? В каких единицах измеряется механическая энергия в СИ?
2. Сформулируйте закон сохранения механической энергии.
3. Как изменяются: а) потенциальная, б) кинетическая, в) механическая энергии системы тел «тело – Земля» при свободном падении тела на этапах «подъем» и «падение»?
4. При каких условиях сохраняется механическая энергия системы тел?

Упражнения

1. С крыши дома высотой h = 45 м отрывается сосулька. Определите скорость сосульки в момент приземления.
2. Модуль скорости приземления свободно падающего вниз камня v_к = 10 м/с. Найдите высоту h₀, с которой падал камень, если его начальная скорость равна нулю.
3. Найдите скорость приземления свободно падающего камня, имевшего на высоте h₀ = 40 м от поверхности Земли скорость v₀ = 10 м/с, направленную вертикально вверх.
4. Шарик бросают с поверхности Земли вертикально вверх так, что |v₀| = 40 м/с. На какой высоте этот шарик будет иметь скорость v_к = 20 м/с?
5. Шарик бросают с поверхности Земли вертикально вверх так, что |v₀| = 40 м/с. Какую скорость будет иметь этот шарик на высоте h_к = 60 м? Куда может быть направлена эта скорость?
6. На гладком горизонтальном полу с помощью бруска массой m = 25 кг удерживают прижатую к стене легкую пружину жесткостью k = 1 МН/м. При этом пружина была сжата из недеформированного состояния на Δl = 1 см. Найдите скорость, которую приобретет брусок после его отпускания к тому моменту, когда на него перестанет действовать пружина.
7. Сформулируйте гипотезу о том, увеличится, уменьшится или не изменится рассчитанный модуль скорости, с которой камень в задаче 1 из текста параграфа подлетит к поверхности Земли, если учитывать силу сопротивления воздуха при падении. Для обоснования ответа определите, положительную или отрицательную работу совершит над телом сила сопротивления воздуха.
8. Выскажите гипотезу, увеличится, уменьшится или не изменится максимальная высота подъема тела, рассчитанная в задаче 2 из текста параграфа, если учитывать сопротивление воздуха движению. Для обоснования ответа определите, положительную или отрицательную работу совершит над телом сила сопротивления воздуха.