Решение задач на вычисление работы сил
Рассмотрим несколько примеров решения задач на вычисление работы сил.
Задача 1. Гоночный автомобиль разгоняется на прямолинейной дороге под действием постоянной силы тяги, значение которой F = 5 кН (рис. 120). Определите работу этой силы при перемещении автомобиля на расстояние L =100 м.
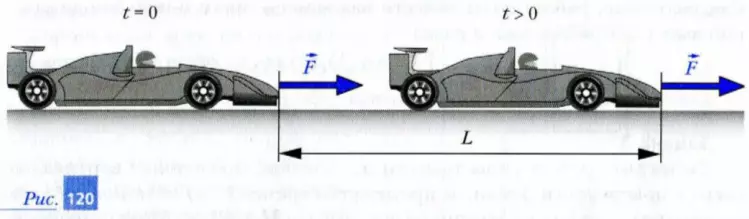
Решение. Поскольку направление силы тяги и направление движения автомобиля совпадают, то
A = F · L = 5000 Н · 100 м = 500000 Дж = 500 кДж = 0,5 МДж.
Ответ: работа силы тяги равна 0,5 МДж.
Отметим, что сила тяги, действующая на автомобиль, создается в результате действия сил трения со стороны дороги на ведущие колеса в направлении движения автомобиля. У гоночных автомобилей с реактивным двигателем она создается непосредственно этим двигателем.
Задача 2. С поверхности Земли вертикально вверх брошен камень, как показано на рис. 121. Какую работу совершит сила тяжести к тому моменту, когда камень поднимется на высоту h = 45 м? Масса камня равна m = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с2.
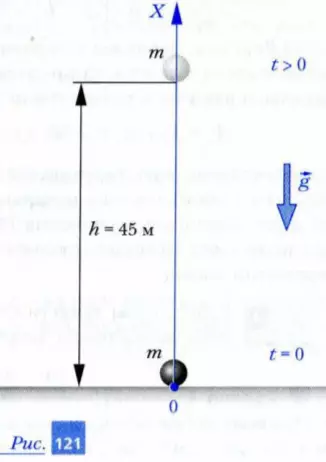
Решение. Поскольку сила тяжести и перемещение камня во время подъема направлены в противоположные стороны, работа силы тяжести будет величиной отрицательной. Как вы помните, модуль силы тяжести равен m · g. Следовательно, работа силы тяжести над камнем при его подъеме до заданной высоты отрицательна и равна
A = -(m · g) · h = -(1 кг · 10 м/с2) · 45 м = -10 Н · 45 м= -450Дж.
Ответ: работа силы тяжести равна -450 Дж.
Задача 3. Вычислите работу силы тяжести над камнем, брошенным вертикально вверх с поверхности Земли, за промежутки времени: а) от момента броска до момента подъема на максимальную высоту H = 60 м; б) от момента достижения максимальной высоты до момента, когда камень окажется на высоте h = 45 м; *в) от момента начала движения с поверхности Земли до момента, когда, опускаясь, камень второй раз за время полета окажется на высоте h = 45 м. Масса камня равна M = 1 кг. Модуль ускорения свободного падения считайте равным g = 10 м/с2.
Решение.
а) Повторяя решение предыдущей задачи, получаем:
Aa = -(M · g) · H = -(1 кг · 10 м/с2) · 60 м = -10 Н · 60 м = -600 Дж.
б) При падении камня из верхней точки направления силы тяжести и движения камня совпадают. Поэтому на этом участке свободного падения работа силы тяжести положительна и равна
Aб = M · g · (H - h) = 10 Н · 15 м = 150 Дж.
*в) Работа силы тяжести в этом случае может быть определена как сумма работ силы тяжести при подъеме камня до верхней точки и при движении камня вниз из верхней точки до высоты h, т. е.
Aв = Aа + Aб = -(M · g) · H + M · g (H - h) = -M · g · h = -450 Дж.
Сопоставим этот результат с результатом из задачи 2. Можно заметить, что в обоих случаях начальные положения камня (поверхность Земли) и его конечные положения (45 м от поверхности Земли) совпадают. При этом сила тяжести совершает одну и ту же работу. Можно сделать следующий вывод.
Работа силы тяжести определяется разностью высот, на которых находилось тело в начальный и конечный моменты времени.
Задача 4. На движущуюся кабину лифта массой M в течение некоторого промежутка времени трос действовал с постоянной силой F. Найдите работу: а) силы F; б) силы тяжести; в) суммы этих сил над кабиной лифта, если за указанный промежуток времени она поднялась вертикально вверх на высоту H.
Решение. Пусть ось Х системы отсчета, связанной с Землей, направлена вертикально вверх, как показано на рис. 122. Тогда значение силы тяжести будет отрицательным, а значение силы F и изменение координаты кабины лифта — положительными.
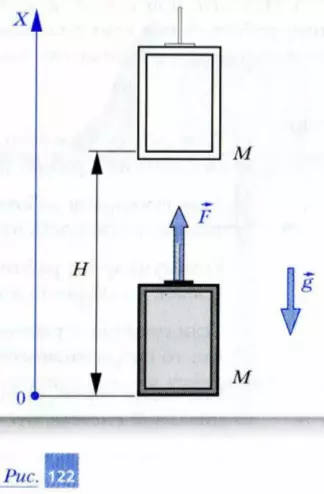
Поэтому работа силы F положительна и равна
Aа = F · H,
а работа силы тяжести — отрицательна и равна
Aб = -M · g · H.
При рассмотрении законов динамики неоднократно подчеркивалось, что при одновременном действии на точечное тело нескольких сил его ускорение будет таким же, как и при действии на это тело одной силы, равной сумме всех действующих на него сил. Заменим действующие на кабину лифта силы одной суммарной. Значение этой силы равно сумме значений силы тяжести и силы F со стороны троса: Fс = F - M · g. Поэтому работа суммарной силы над кабиной при ее перемещении на высоту H равна
Aв = Fс · H = (F - M · g) · H = F · H - M · g · H = Aа + Aб.
При одновременном действии на тело нескольких сил их суммарная работа равна сумме работ этих сил.
Таким образом, для рассмотренного случая можно сделать следующие выводы.
1. При F > M · g суммарная работа этих сил положительна. Поэтому, если на кабину не действуют другие силы, она должна разгоняться, т. е. ее ускорение должно быть положительным. Это же заключение легко сделать и непосредственно из второго закона Ньютона.
2. При F = M · g суммарная сила равна нулю. Поэтому и суммарная работа этих сил равна нулю. Кабина будет двигаться без ускорения, т. е. ее скорость не будет изменяться.
3. Наконец, при F
Итоги
Если на точечное тело одновременно действуют несколько сил, их суммарная работа равна сумме работ этих сил.
Если суммарная работа всех действующих на тело сил положительна, то скорость этого тела увеличивается.
Если суммарная работа всех действующих на тело сил отрицательна, то скорость этого тела уменьшается.
Если суммарная работа всех действующих на тело сил равна нулю, то скорость этого тела остается неизменной.
Сказанное верно, если движение тела рассматривается в инерциальной системе отсчета.
Упражнения
1. Найдите работу силы трения, тормозящей грузовой автомобиль на отрезке пути L = 40 м, если модуль силы равен 25 кН.
2. Определите работу силы тяжести над камнем массой m = 5 кг при его падении с высоты h = 80 м на Землю.
3. Найдите работу пороховых газов над пулей к моменту ее вылета из ствола снайперской винтовки длиной L = 1 м. Считайте, что сила действия газов постоянна и ее модуль равен 5 кН. Винтовку во время выстрела удерживает неподвижной стоящий на Земле человек.
4. Определите работу силы тяжести над свободно падающим камнем массой m = 1 кг за промежуток времени, в течение которого скорость камня изменяется от v0 = 0 до vк = 30 м/с.
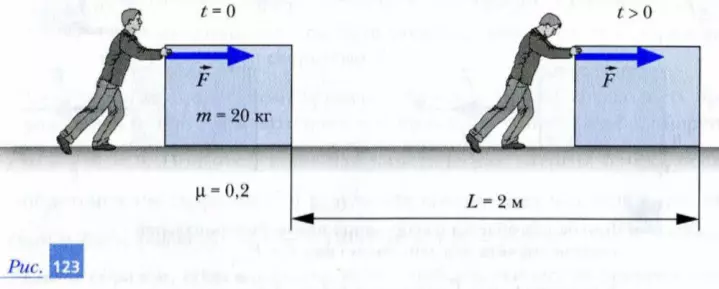
5. Мальчик действует на движущийся по горизонтальному полу ящик массой m = 20 кг силой, направленной в сторону движения ящика (рис. 123) и равной по модулю 50 Н. Коэффициент трения ящика о пол μ = 0,2. При этом за некоторое время ящик передвинулся на расстояние L = 2 м. Какую работу за это время совершат: а) мальчик; б) сила тяжести; в) сила трения; г) сумма всех сил, действующих на ящик? Увеличится или уменьшится скорость ящика за это время?