Применение уравнения состояния идеального газа к различным процессам

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один из трех параметров – p, V или T – остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра называют газовыми законами.

Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами. (От греческого слова «изос» – равный.) Изопроцессы широко распространены в природе и часто используются в технике.

Изотермический процесс. Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим. Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой – термостатом. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении процесса.

Согласно уравнению состояния идеального газа (3.4) в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же: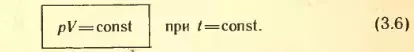

Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется.

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Поэтому он носит название закона Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха). Лишь при давлениях, в несколько тысяч раз больших атмосферного, отклонения от этого закона становятся существенными.

Убедиться в справедливости закона Бойля-Мариотта при давлениях, близких к атмосферному, можно с помощью установки, описанной в предыдущем параграфе.

Зависимость давления газа от объема при постоянной температуре изображается графически кривой, которая носит название изотермы (рис 32). Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой. Разным постоянным температурам соответствуют различные изотермы. При повышении температуры давление согласно уравнению состояния (3.4) увеличивается, если V – const. Поэтому изотерма, соответствующая более высокой температуре T₂ лежит выше изотермы, соответствующей белее низкой температуре T₁.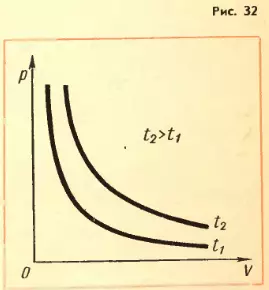

Изобарный процесс. Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным. (От греческого слова «барос» – тяжесть, вес.)

Из уравнения состояния идеального газа (3.4) вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур. Действительно, для первого состояния: 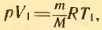, для второго состояния: 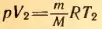(давление постоянно). Отсюда, разделив первое уравнение на второе, получим:

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (p₀ – нормальное атмосферное давление, T₀ = 273 К – температура таяния льда, V₀ – объем при этих условиях), V₁ и T₁ обозначить через V и T, то из (3.7) следует: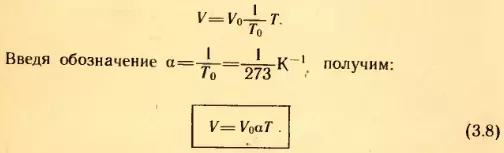

Этот газовый закон был установлен экспериментально в 1802 г. французским ученым Гей-Люссаком и носит название закона Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.

Коэффициент α называют температурным коэффициентом объемного расширения газов. Все газы увеличивают свой объем на 1/273 часть того объема, который каждый из газов занимал при 273 К (0°C), если температура меняется на 1 К.

Зависимость объема газа от температуры при постоянном давлении изображается графически прямой, которая называется изобарой (рис. 33).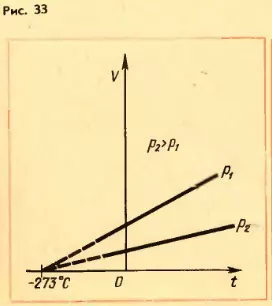

Различным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно закону Бойля-Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению p₂, лежит ниже изобары, соответствующей более низкому давлению p₁.

В области низких температур все изобары идеального газа пересекаются в точке T=0. Но это не означает, что объем реального газа действительно обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (3.4) не применимо.

Изохорный процесс. Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным. (От греческого слова «хорема» – вместимость.)

Из уравнения состояния (3.4) вытекает, что отношение давлений газа данной массы при постоянном объеме равно отношению его абсолютных температур:

Если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, а p₁ и T₁ обозначить через p и T, то из (3.9) следует: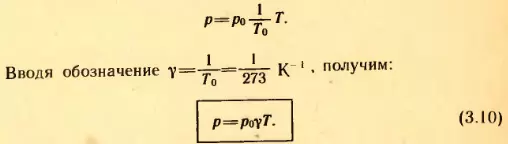

Этот газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Коэффициент γ (равный температурному коэффициенту объемного расширения α) называют температурным коэффициентом давления газа. Он одинаков для всех газов. Все газы увеличивают свое давление на 1/273 того давления, которое каждый из газов имел при 273 К (0°C), если температура возрастает на 1 К.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (рис. 34). Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля-Мариотта падает. Поэтому изохора, соответствующая большему объему V₂, лежит ниже изохоры, соответствующей объему V₁.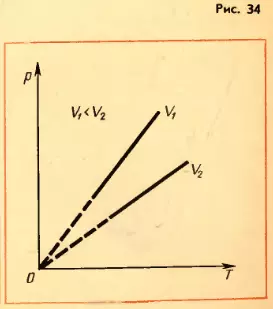

В соответствии с уравнением (3.10) все изохоры начинаются в точке T = 0. Значит, давление идеального газа при абсолютном нуле равно нулю.