Примеры решения задач к главе "Уравнение состояния идеального газа. Газовые законы"

В задачах на использование газовых законов встречаются обычно следующие ситуации:

а) известны макроскопические параметры в начальном состоянии газа и некоторые параметры в конечном состоянии.

Если при переходе из начального состояния в конечное один из параметров не меняется, то при изотермическом процессе можно пользоваться законом Бойля-Мариотта в форме (3.6) или в эквивалентной форме 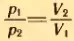, следующей из (З.6). При изобарном процессе нужно пользоваться законом Гей-Люссака (3.8) или (3.7); при изохорном – законом Шарля (3.10) или (3.9).

Если меняются все три параметра, то надо использовать уравнение состояния (3.4) или (3.5);

б) известна часть макроскопических параметров в определенном состоянии газа. Надо найти неизвестные величины. В этих случаях удобнее всего пользоваться уравнением Менделеева-Клапейрона (3.4);

в) во многих задачах требуется построение графиков, изображавших разного рода процессы. Для построения графиков нужно знать зависимость параметров друг от друга. Эта зависимость в общем случае дается уравнением состояния, а в частных случаях – газовыми законами.

При решении всех задач надо четко представлять себе, каково начальное состояние системы и какого рода процесс переводит ее в конечное состояние.

1. Баллон вместимостью V₁ = 0,02 м³, содержавший воздух под давлением p₁ = 4 * 10⁵ Па, соединяют с баллоном вместимостью V₂ = 0,06 м³, из которого воздух выкачан. Найти давление p, установившееся в сосудах. Температура постоянна.

Решение. Воздух из первого баллона займет весь предоставленный ему объем V₁ + V₂. По закону Бойля-Мариотта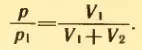

Отсюда искомое давление равно:

2. На какую долю первоначального объема увеличится объем газа, находящегося при температуре t = 27°C, если нагреть его на 1°C при постоянном давлении?

Решение. Пусть V₁ и T₁ = 273 К + t = 300 К – первоначальные значения параметров состояния газа, V₂ и T₂ = T₁ + 1 К – конечные значения тех же параметров.

По закону Гей-Люссака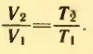

Равенство не изменится, если из левой и правой частей вычесть по единице: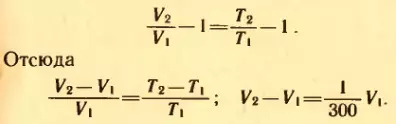

Объем газа увеличится на 1/300 долю первоначального.

3. Плотность воздуха при нормальных условиях (т. е. при t₀ = 0°C и нормальном атмосферном давлении p₀ = 101325 Па) ρ = 1,29 кг/м³. Найти среднюю молярную массу M воздуха.

Решение. Уравнение состояния идеального газа при нормальных условиях имеет вид: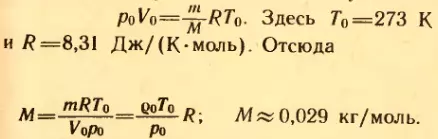

4. Построить изобары для 2 г водорода при нормальном атмосферном давлении p₀ в осях p, T; p, V; V, T.

Решение. На графиках зависимости p от T и p от V изобара будет представлять собой прямую, параллельную либо оси T, либо оси V (рис. 37, а и б).