Идеальный газ в молекулярно-кинетической теории

Идеальный газ. Идеальный газ с точки зрения молекулярно-кинетической теории простейшая физическая модель реального газа.

Под моделью в физике понимают не увеличенную или уменьшенную копию реального объекта. Физическая модель – это создаваемая учеными общая картина реальной системы или явления, которая отражает наиболее существенные, наиболее характерные свойства системы.

В физической модели газа принимаются во внимание лишь те основные свойства молекул, учет которых необходим для объяснения главных закономерностей поведения реального газа в определенных интервалах давления и температуры.

В молекулярно-кинетической теории идеальным газом называют газ, состоящий из молекул, взаимодействие между которыми пренебрежимо мало. Иными словами, предполагается, что средняя кинетическая энергия молекул идеального газа во много раз больше потенциальной энергии их взаимодействия.

Реальные газы ведут себя подобно идеальному газу при достаточно больших разрежениях, т. е. когда среднее расстояние между молекулами во много раз больше их размеров. В этом случае силами притяжения между молекулами можно полностью пренебречь. Силы же отталкивания проявляются лишь на ничтожно малых интервалах времени при столкновениях молекул друг с другом.

В простейшей модели газа молекулы рассматривают как очень маленькие твердые шарики, обладающие массой. Движение отдельных молекул подчиняется законам механики Ньютона. Конечно, нет никакой гарантии, что с помощью такой модели можно объяснить все процессы в разреженных газах. Ведь известно, что молекулы отличаются не только массами. Они имеют сложное строение.

Но сейчас мы поставим и будем решать достаточно узкую задачу: вычислим давление газа с помощью молекулярно-кинетической теории. Для этой задачи простейшая модель газа оказывается удовлетворительной. Она приводит к результатам, которые подтверждаются опытом.

Давление газа в молекулярно-кинетической теории. Пусть газ находится в закрытом сосуде. Манометр показывает давление газа p0. (Напомним: давление определяется отношением модуля F силы, действующей перпендикулярно поверхности, к площади поверхности S: 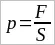. Давление выражается в паскалях или миллиметрах ртутного столба: 1 Па = 1 Н/м² = 7,5 · 10^–³ мм рт. ст.) Но как возникает это давление? Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на нее с определенной силой. В результате беспорядочных ударов о стенку сила, действующая со стороны всех молекул на единицу площади стенки, т. е. давление, будет быстро меняться со временем примерно так, как показано на рисунке 18. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади его чувствительного элемента – мембраны. Несмотря на небольшие изменения давления, среднее значение давления p0 практически оказывается вполне определенной величиной, так как ударов о стенку очень много, а массы молекул очень малы.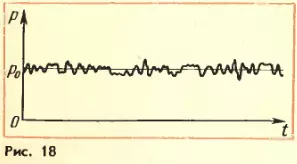

Давление газа будет тем больше, чем больше молекул ударяется о стенку за некоторый интервал времени и чем больше скорости соударяющихся со стенкой молекул.
Возникновение давления газа можно пояснить с помощью простой механической модели. Возьмем диск (он играет роль мембраны манометра) и закрепим его на стержне так, чтобы он располагался вертикально и мог поворачиваться вместе со стержнем вокруг вертикальной оси (рис. 19). С помощью наклонного желоба на диск направим струйку мелкой дроби (дробинки играют роль молекул). В результате многочисленных ударов дробинок на диск будет действовать некоторая средняя сила, вызывающая поворот стержня и изгиб упругой пластины П. Эффект же от ударов отдельных дробинок не заметен.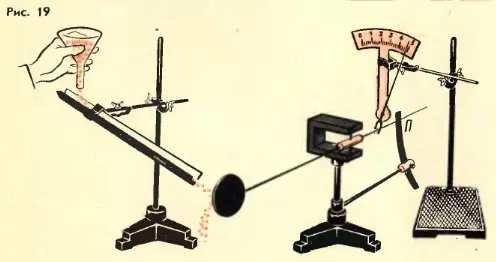

Тепловое движение молекул. С самого начала нужно отказаться от попыток проследить за движением всех молекул, из которых состоит газ. Их слишком много, и из-за столкновений друг с другом они движутся очень сложно. Нам и не нужно знать, как движется каждая молекула. Мы должны выяснить, к какому результату приводит совокупное движение всех молекул.

Характер же движения всей совокупности молекул газа известен из опыта (см. § З). Молекулы участвуют в хаотическом (тепловом) движении. Это означает, что скорость любой молекулы может оказаться как очень большой, так и очень малой, а направление движении молекул беспрестанно меняется при их столкновениям друг с другом.

Скорости отдельных молекул могут быть любыми, однако среднее значение модуля их скорости вполне определенное. Точно так же рост учеников в классе не одинаков. Но среднее значение роста – определенная величина. Чтобы ее найти, надо сложить вместе рост учеников и разделить эту сумму на количество учеников.

Среднее значение квадрата модуля скорости. В дальнейшем нам понадобится среднее значение не самой скорости, а квадрата скорости, от которого зависит средняя кинетическая энергия молекул.

Обозначим модули скоростей отдельных молекул через v₁, v₂, v₃, …, v_N. Среднее значение квадрата скорости определится следующей формулой:

Действительно, для каждой молекулы справедливо выражение (1.9). Сложив эти выражения для отдельных молекул и разделив обе части полученного уравнения на число молекул N, мы придем к формуле (1.10).

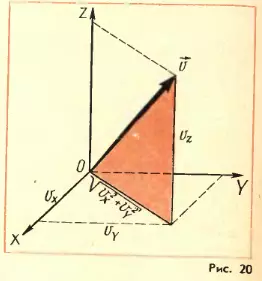
Так как направления Ox, Oy и Oz вследствие хаотичности движения молекул равноправны, средние значения квадратов проекций скорости равны друг другу: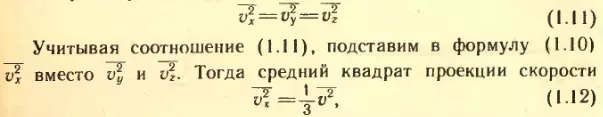

т.е. средний квадрат проекции скорости равен 1/3 среднего квадрата самой скорости. Множитель 1/3 появляется вследствие трехмерности пространства и, соответственно, существования трех проекций у любого вектора.