Вращательное движение

Расскажу вам о вращательном движении.

На первый взгляд может даже показаться, что вращательное движение нарушает законы механики.

В чем же нарушение и каких законов? Ну, скажем, закон инерции. Ведь всякое тело, если на него не действуют уравновешенные силы, должно или покоиться, или двигаться равномерно и прямолинейно. Но вот я даю боковой толчок этому глобусу, и он начинает вращаться. Если бы не трение, он, вероятно, вращался бы вечно, как вращается земной шар, никем не подталкиваемый. Как же быть с первым законом Ньютона? Или есть два закона инерции: одни для прямолинейного, а другой для вращательного движения?

Не торопитесь, мы сейчас выясним, в чем тут дело, и убедимся, что беспокоиться за законы Ньютона не приходится.

Вращательное движение отличается от поступательного. Однако есть в них и много общего, и весьма полезно сопоставить эти два вида движения. Много путаницы в головах учащихся происходит оттого, что в курсе физики средней школы не строго разграничивают механику материальной точки и механику материального тела. Скажите, вы помните, что называется поступательным движением?

– Конечно. Движение тела, при котором все его точки движутся одинаково.

– А как вы это понимаете?

– Я понимаю это так, что все точки тела в каждый момент времени имеют одинаковую по модулю и направлению скорость. Все точки описывают одинаковые траектории.

– Вот именно. Поэтому и можно рассматривать поступательное движение тела как движение одной точки, вернее, заменить движение тела движением его центра масс. Если на такое тело (материальную точку) не действуют другие тела, т. е. если оно не испытывает на себе действия неуравновешенных сил, то оно покоится или движется равномерно и прямолинейно.

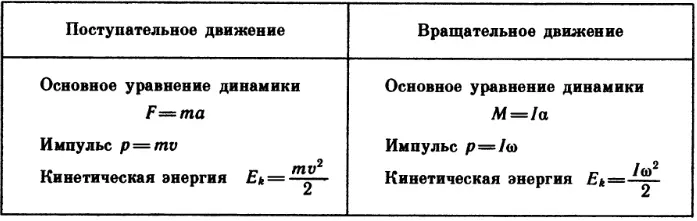
Вращение тела характеризуют угловой скоростью, показывающей, на какой угол оно повернется за единицу времени. В технике угловую скорость часто выражают числом оборотов в минуту. Если угловая скорость постоянна, то мы говорим, что тело вращается равномерно. Если угловая скорость равномерно возрастает, то вращение называют равноускоренным. Сходство законов поступательного и вращательного движения поразительное. Только буквенные обозначения различны, а формулы получаются совершенно одинаковые. Вот первая параллель: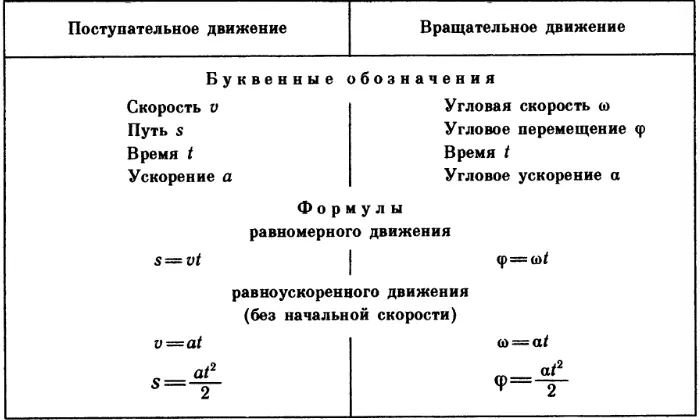

Все задачи по кинематике как вращательного, так и поступательного движения решаются по этим формулам аналогично.

– Это все понятно. Но как же быть с законом Ньютона?

– Не торопитесь, слушайте дальше. Рассмотрим движение одной материальной точки. Если хотите, вы можете представить себе ее как маленький тяжелый шарик. Можно сделать так, чтобы он двигался по окружности? (Катим маленький шарик от шарикоподшипника по столу.)

– Конечно, нет, он катится по прямой.

Можно, конечно, вести шарик по окружности, поддерживая его все время пальцами. Но стоит только убрать руку, как он будет продолжать движение по прямой линии.

– Итак, материальная точка может двигаться по окружности только под действием силы. Я вел шарик рукой, можно было бы привязать к нему веревочку или катить его внутри желобка. Как только прекратится действие силы, шарик начнет двигаться прямолинейно и равномерно.

В твердом теле не одна точка, а множество. Как вы думаете, они (точки) свободны или связаны?

– На них действует сила сцепления.

– Верно. Они-то и удерживают точки на круговой орбите. Не будь этих сил, материальные точки вращающегося тела разлетелись бы, как грязь слетает с вращающихся колес.

Есть еще одно сходство между поступательным и вращательным движением. При поступательном движении все точки тела движутся в данный момент времени с одинаковой линейной скоростью v. Если тело вращается, тоо все точки вращающегося тела движутся с одинаковой угловой скоростью ω.

Например, угловые скорости всех точек вращающейся спицы AB (рис. 59) одинаковы, а линейные различны.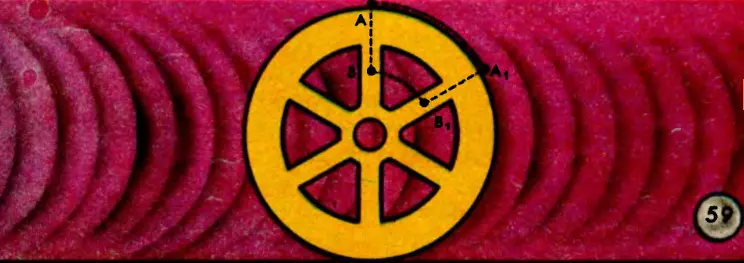

На уроке физики вам говорили. Что равномерное движение точки по окружность есть в то же время движение с ускорением. Это ускорение называется центростремительным ускорением. Оно не характеризует изменение скорости по модулю, а характеризует только изменение направления скорости. Тут нелегко разобраться.

Я бы отстаивал определение равномерного вращательного движения только по угловой скорости. Тогда те параллельные формулы, о которых я говорил, будут всем понятны. Да и в технике, когда речь идет о равномерном вращении маховика или ротора электрического генератора или двигателя, подразумевают постоянной угловую скорость. Постоянное число оборотов якоря генератора обеспечивает постоянное напряжение в сети; постоянное число оборотов маховика обеспечивает плавный ход машины и экономичность ее работы. Это постоянство стараются поддержать, регулируя работу машины.

Теперь проведем параллель динамическую. По второму закону Ньютона ускорение, получаемое телом, вычисляется из формулы a = F/m. При вращении тела изменение угловой скорости будет зависеть от силы. Теперь скажите, все ли равно, где приложить силу при завинчивании, скажем, гайки: к концу рукоятки гаечного ключа или к самой гайке?

Вращающее действие силы, или момент силы, – вот что здесь важно, вот что является аналогом силы поступательного движения. Параллель найдена: силе в поступательном движении соответствует момент силы во вращательном движении. Так продолжим нашу сравнительную табличку.

– Я еще не написал формулу второго закона Ньютона, потому что об этом законе следует сказать подробнее. В формулу закона Ньютона входит масса m. Что она характеризует?

– Инертность тела.

– Правильно. Теперь подумайте, характеризует ли масса инертность вращающегося тела?

– Инертность вращающегося тела характеризуется не массой, а особой величиной, называемой моментом инерции, в которую входит как составная часть и масса. Момент инерции обозначается буквой I. Он зависит от массы тела и распределения этой массы, т. е. от формы тела. Тела различной формы имеют различные моменты инерции.

Простейший случай — движение материальной точки по окружности. Момент инерции такой точки равен произведению массы точки на квадрат расстояние ее от оси вращения, т. е. I = mr². Если массу отнести от оси вращения на расстояние, вдвое большее, то инертность этой массы, или устойчивость вращательного движения, будет больше в четыре раза. Вот почему маховые колеса делают большими. Но слишком увеличивать радиус нельзя. С увеличением радиуса колеса увеличивается линейная скорость точек обода колеса: v = ωr. Учитывая, что центростремительное ускорение есть a = v²/r, получаем отсюда: a = ω²r. Это означает, что с увеличением радиуса колеса растет центростремительное ускорение точек его обода. Создающая это ускорение сила сцепления молекул может оказаться недостаточной для удержания их на круговом пути, и тогда колесо разрушится.

Каждое тело можно представить состоящим из множества точек. Для вычисления момента инерции тела надо суммировать моменты инерции отдельных точек. Эта задача вам пока не под силу. Скажу только, что для диска и сплошного цилиндра, вращающихся вокруг собственной оси, I = ½ mr². В телах такой формы разные точки тела находятся на разных расстояниях от оси вращения, начиная от 0 и до r. Момент инерции тонкого круглого кольца (есть сходство с ободом маховика) I = mr². Обо всем этом вы узнаете из курса теоретической механики, когда будете учиться в техникуме или институте. Сейчас же вы должны понять, что во вращательном движении роль массы играет момент инерции и закон динамики вращательного движения, аналогичный второму закону Ньютона, примет вид: M = Iα. Теперь мы можем закончить сравнительную таблицу, включив в нее формулы для основного уравнения динамики, импульса и кинетической энергии: