Закон сохранения энергии

В общем случае тело обладает одновременно как кинетической, так и потенциальной энергией. Их сумму называют полной механической энергией:

   E = E_к + E_п      (15.1)

Это понятие было введено в 1847 г. 26-летним немецким ученым Г. Гельмгольцем.

Что происходит с полной механической энергией по мере движения тела? Чтобы выяснить это, рассмотрим простое явление.

Бросим вертикально вверх мяч. Придав мячу скорость, мы тем самым сообщим ему некоторую кинетическую энергию. По мере движения мяча вверх его движение будет замедляться притяжением Земли и скорость, а вместе с ней и кинетическая энергия мяча будут становиться все меньше и меньше. Потенциальная же энергия мяча вместе с высотой h будет при этом возрастать. В высшей точке траектории (на максимальной высоте) потенциальная энергия мяча достигнет своего наибольшего значения, а кинетическая энергия окажется равной нулю. После этого мяч начнет падать вниз, постепенно набирая скорость. Кинетическая энергия при этом начнет увеличиваться, а потенциальная энергия (из-за уменьшения высоты) — убывать. В момент удара о землю кинетическая энергия мяча достигнет максимального значения, а потенциальная энергия обратится в нуль.

Итак, когда кинетическая энергия тела уменьшается, потенциальная энергия возрастает, и наоборот, когда кинетическая энергия тела увеличивается, его потенциальная энергия убывает. Изучение свободного падения тела (в отсутствие сопротивления воздуха) показывает, что всякое уменьшение одного из этих видов энергии сопровождается равным увеличением другого вида энергии. Полная же механическая энергия тела при этом сохраняется. В этом состоит закон сохранения механической энергии:

Полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.

Если обозначить начальную и конечную энергии тела через E и E', то закон сохранения энергии можно выразить в виде следующего равенства:

   E' = E.        (15.2)

Предположим, что свободно движущееся тело в начальный момент времени находилось на высоте h0 и имело при этом скорость v0. Тогда его полная механическая энергия в этот момент времени была равна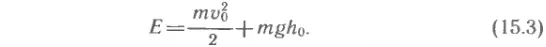

Если спустя некоторое время рассматриваемое тело окажется на высоте h, имея скорость v (рис. 28), то его полная механическая энергия станет равной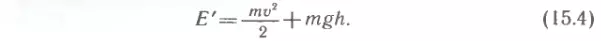

Согласно закону сохранения энергии, оба эти значения энергии должны совпадать. Поэтому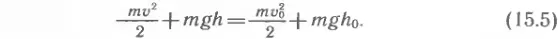

Если начальные значения h0 и v0 известны, то это уравнение позволяет найти скорость тела v на высоте h или, наоборот, высоту h, на которой тело будет иметь заданную скорость v. Масса тела при этом никакой роли играть не будет, так как в уравнении (15.5) она сокращается.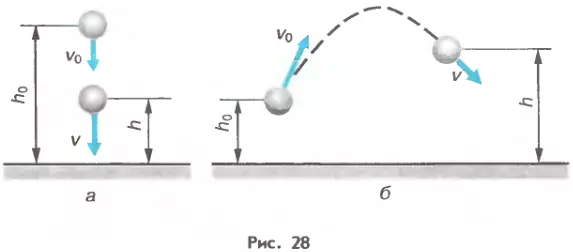

Следует помнить, что полная механическая энергия сохраняется лишь тогда, когда отсутствуют силы трения и сопротивления. Если же эти силы присутствуют, то их действие приводит к уменьшению механической энергии.

1. Что называют полной механической энергией? 2. Сформулируйте закон сохранения механической энергии. 3. С какой энергией — кинетической или потенциальной — совпадает полная механическая энергия свободно падающего тела в момент удара о землю? 4. С какой энергией совпадает полная механическая энергия брошенного вертикально вверх мяча в момент, когда он оказывается в высшей точке своего полета? 5. Что происходит с полной механической энергией тела при наличии сил трения и сопротивления?