Реактивное движение

Законы Ньютона позволяют объяснить очень важное механическое явление — реактивное движение. Так называют движение тела, возникающее при отделении от него с какой-либо скоростью некоторой его части.

Возьмем, например, детский резиновый шарик, надуем его и отпустим. Мы увидим, что, когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Это и есть реактивное движение.

По принципу реактивного движения передвигаются некоторые представители животного мира, например кальмары и осьминоги. Периодически выбрасывая вбираемую в себя воду, они способны развивать скорость до 60—70 км/ч. Аналогичным образом перемещаются медузы, каракатицы и некоторые другие животные.

Примеры реактивного движения можно обнаружить и в мире растений. Например, созревшие плоды «бешеного» огурца при самом легком прикосновении отскакивают от плодоножки и из отверстия, образовавшегося на месте отделившейся ножки, с силой выбрасывается горькая жидкость с семенами; сами огурцы при этом отлетают в противоположном направлении.

Реактивное движение, возникающее при выбросе воды, можно наблюдать на следующем опыте. Нальем воду в стеклянную воронку, соединенную с резиновой трубкой, имеющей Г-образный наконечник (рис. 20). Мы увидим, что, когда вода начнет выливаться из трубки, сама трубка придет в движение и отклонится в сторону, противоположную направлению вытекания воды.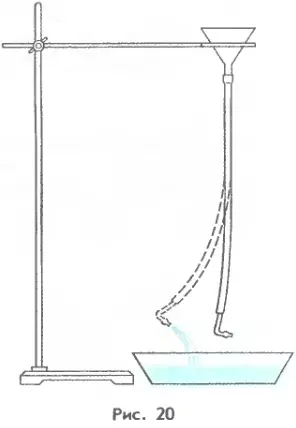

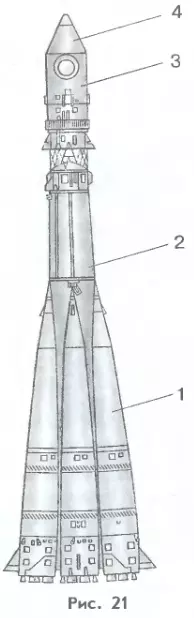
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат, состоящий из сотен тысяч и миллионов деталей. Масса ракеты огромна. Она складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.

«Сухая» масса ракеты, в свою очередь, состоит из массы конструкции (т. е. оболочки ракеты, ее двигателей и системы управления) и массы полезной нагрузки (т.е. научной аппаратуры, корпуса выводимого на орбиту космического аппарата, экипажа и системы жизнеобеспечения корабля).

По мере истечения рабочего тела освободившиеся баки, лишние части оболочки и т. д. начинают обременять ракету ненужным грузом, затрудняя ее разгон. Поэтому для достижения космических скоростей применяют составные (или многоступенчатые) ракеты (рис. 21). Сначала в таких ракетах работают лишь блоки первой ступени 1. Когда запасы топлива в них кончаются, они отделяются и включается вторая ступень 2; после исчерпания в ней топлива она также отделяется и включается третья ступень 3. Находящийся в головной части ракеты спутник или какой-либо другой космический аппарат укрыт головным обтекателем 4, обтекаемая форма которого способствует уменьшению сопротивления воздуха при полете ракеты в атмосфере Земли.

Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Почему это происходит?

Согласно третьему закону Ньютона, сила F, с которой ракета действует на рабочее тело, равна по величине и противоположна по направлению силе F', с которой рабочее тело действует на корпус ракеты:

        F' = F.          (12.1)

Сила F' (которую называют реактивной силой) и разгоняет ракету.

Из равенства (10.1) следует, что сообщаемый телу импульс равен произведению силы на время ее действия. Поэтому одинаковые силы, действующие в течение одного и того же времени, сообщают телам равные импульсы. В данном случае импульс m_рv_р, приобретаемый ракетой, должен пульсу m_газv_газ выброшенных газов:

m_рv_р = m_газv_газ

Отсюда следует, что скорость ракеты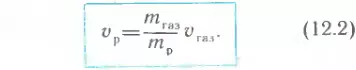

Проанализируем полученное выражение. Мы видим, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и чем больше отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.

Формула (12.2) является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты впервые была получена в 1897 г. К. Э. Циолковским и потому носит его имя.

Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости. В таблице 3 приведены отношения начальной массы ракеты m0 к ее конечной массе m, соответствующие разным скоростям ракеты при скорости газовой струи (относительно ракеты) v = 4 км/с.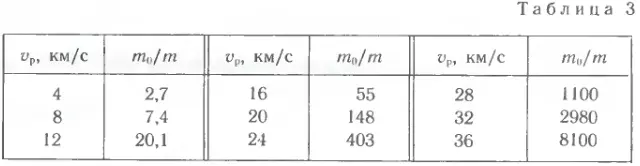

Например, для сообщения ракете скорости, превышающей скорость истечения газов в 4 раза (v_р=16 км/с), необходимо, чтобы начальная масса ракеты (вместе с топливом) превосходила конечную («сухую») массу ракеты в 55 раз (m₀/m = 55). Это означает, что львиную долю от всей массы ракеты на старте должна составлять именно масса топлива. Полезная же нагрузка по сравнению с ней должна иметь очень малую массу.

Важный вклад в развитие теории реактивного движения внес современник К. Э. Циолковского русский ученый И. В. Мещерский (1859—1935). Его именем названо уравнение движения тела с переменной массой.

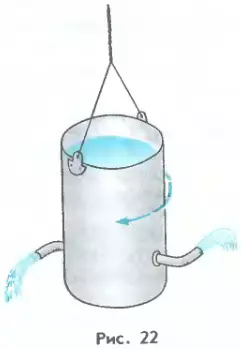
1. Что такое реактивное движение? Приведите примеры. 2. В опыте, изображенном на рисунке 22, при вытекании воды через изогнутые трубки ведерко вращается в направлении, указанном стрелкой. Объясните явление. 3. От чего зависит скорость, приобретаемая ракетой после сгорания топлива?