Абсолютная температура. Температура – мера средней кинетической энергии молекул

Абсолютный нуль температуры. Температура, определяемая формулой (2.6), очевидно, не может быть отрицательной, так как все величины, стоящие в левой чисти (2.6), заведомо положительны. Следовательно, наименьшее возможное значение температуры T есть T = 0, когда либо давление p, либо объем V равны нулю. Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объеме или объем идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулем температуры. Это самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказывал Ломоносов.

Абсолютная шкала температур. Английский ученый У. Кельвин ввел абсолютную шкалу температур. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.

Единица абсолютной температуры в СИ называется кельвином (обозначается буквой K).

Постоянная Больцмана. Определим коэффициент k в формуле (2.6) так, чтобы один кельвин равнялся градусу по шкале Цельсия.

Мы знаем значения Θ при 0°C и 100°C (формулы 2.2 и 2.4). Обозначим абсолютную температуру при 0°C через T₁, а при 100°C через T₂. Тогда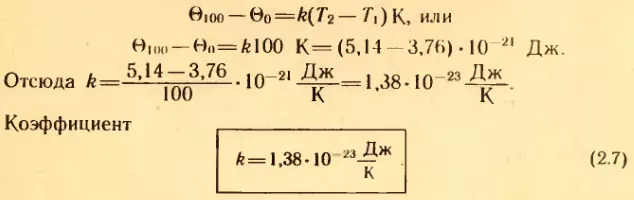

называется постоянной Больцмана в честь великого австрийского физика Л. Больцмана, одного из основателей молекулярно-кинетической теории газов.

Постоянная Больцмана связывает температуру Θ в энергетических единицах с температурой T в кельвинах. Это одна из наиболее важных постоянных молекулярно-кинетической теории.

Больцман Людвиг (1844–1906) — великий австрийский физик, один из основоположников молекулярно-кинетической теории. В трудам Больцмана молекулярно-кинетическая теория впервые предстала как логически стройная, последовательная физическая теория. Больцман много сделал для развития и популяризации теории электромагнитного поля Максвелла. Борец по натуре, он страстно отстаивал необходимость молекулярного истолкования тепловых явлений и принял на себя основную тяжесть борьбы с учеными, отрицавшими существование молекул.

Связь абсолютной шкалы и шкалы Цельсия. Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдем сначала значение абсолютной температуры, соответствующее 0°C.

Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры T будет на 273 градуса выше соответствующей температуры t по Цельсию:

T = t + 273.     (2.8)

Но изменение абсолютной температуры ΔT равно изменению температуры по шкале Цельсия Δt: ΔT = Δt.

На рисунке 27 для сравнения изображены абсолютная шкала и шкала Цельсия. Абсолютному нулю соответствует температура t = –273°C. (Более точное значение абсолютного нуля: –273,15°C.)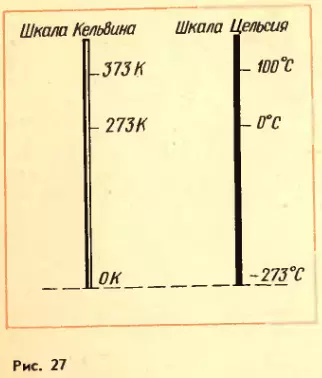

Температура – мера средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории в форме (2.1) и определения температуры (2.6) вытекает важнейшее следствие: абсолютная температура есть мера средней кинетической энергии движения молекул. Докажем это.

Левые части уравнений 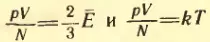одинаковы. Значит, должны быть равны и их правые части. Отсюда вытекает связь между средней кинетической энергией поступательного движения молекул и температурой: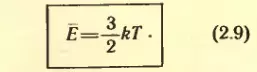

Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре. Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надежное обоснование.

Соотношение между температурой и средней кинетической энергией поступательного движения молекул (2.9) установлено для разреженных газов. Однако оно оказывается справедливым для любых веществ, движение атомов или молекул которых подчиняется законам механики Ньютона. Оно верно для жидкостей и твердых тел, у которых атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решетки.
При приближении температуры к абсолютному нулю энергия теплового движения молекул также приближается к нулю.

Зависимость давления газа от его концентрации и температуры. Подставляя (2.9) в формулу (1.18), получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:

Из формулы (2.10) (эту формулу можно также получить из уравнения (2.6)) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный вам из курса химии VIII класса: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

1. Какие свойства макроскопических тел используются для измерения температуры? 2. В чем преимущество использования разреженных газов для измерения температуры? 3. Как связаны объем, давление и число молекул различных газов в состоянии теплового равновесия? 4. Каков физический смысл постоянной Больцмана? 5. Какие преимущества имеет абсолютная шкала температур по сравнению с другими шкалами? 6. Чему равен абсолютный нуль температуры по шкале Цельсия? 7. Как зависит от температуры средняя кинетическая энергия поступательного движения молекул? 8. Как связано давление газа с его температурой и концентрацией молекул? 9. Каков физический смысл абсолютного нуля температуры?