Измерение температуры

Термометры. Для измерения температуры можно воспользоваться изменением любой макроскопической величины в зависимости от температуры: объема, давления, электрического сопротивления и т. д.

Чаще всего на практике используют зависимость объема жидкости (ртути или спирта) от изменения температуры. При градуировке термометра обычно за начало отсчета (0) принимают температуру тающего льда; второй постоянной точкой (100) считают температуру кипения воды при нормальном атмосферном давлении (шкала Цельсия). Шкалу между точками 0 и 100 делят на 100 равных частей, называемых градусами (рис. 25). Перемещение столбика жидкости на одно деление соответствует изменению температуры на 1° C.

Так как различные жидкости расширяются при нагревании не совсем одинаково, то установленная таким образом шкала будет до некоторой степени зависеть от свойств жидкости. 0 и 100° C будут, конечно, совпадать у всех термометров, но, скажем, 50° C совпадать не будут.

Какое же вещество выбрать, для того чтобы избавиться от этой зависимости? Было замечено, что в отличие от жидкостей все разреженные газы – водород, гелий, кислород – расширяются при нагревании одинаковым образом и одинаково меняют свое давление при изменении температуры. По этой причине в физике для установления рациональной температурной шкалы используют изменение давления определенного количества разреженного газа при постоянном объеме или изменение объема газа при постоянном давлении. Такую шкалу иногда называют идеальной газовой шкалой температур. При ее установлении удается избавиться еще от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчета, т. е. нулевой температуры. Ведь за начало отсчета вместо температуры таяния льда с тем же успехом , можно было бы взять температуру кипения воды.

Сейчас мы подробно рассмотрим, как можно использовать разреженные газы для определения температуры.

Газы в состоянии теплового равновесия. Возьмем несколько сосудов, заполненных различными газами, например водородом, гелием и кислородом. Сосуды имеют определенные известные объемы и снабжены манометрами. Это позволяет измерять давление в каждом из сосудов.

Количество газа ν в любом сосуде тоже известно. Тем самым известно и число молекул N в каждом сосуде. Согласно формулам (1.3), (1.7)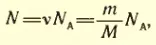

где N_A – постоянная Авогадро, m – масса газа, а M – его малярная масса.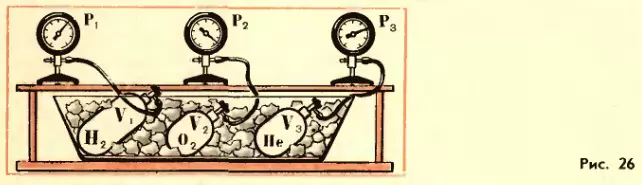

Приведем газы в состояние теплового равновесия. Для этого поместим сосуды в тающий лед и подождем, пока не установится равновесие и давление газов перестанет меняться (рис. 26). После этого можно утверждать, что все газы имеют одинаковую температуру 0° C. Но, разумеется, давления газов p, их объемы V и числа молекул N будут различными.

Можно, однако, ожидать, что между p, V, N одного газа и теми же величинами любого другого газа должна существовать связь, если только температуры газов одинаковы. На это указывает основное уравнение молекулярно-кинетической теории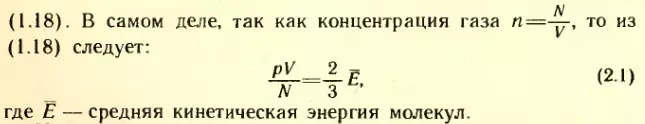

Из курса физики VI класса известно, что, чем быстрее движутся молекулы, тем выше их температура. Естественно предположить, что при тепловом равновесии средние кинетические энергии молекул всех газов одинаковы. А это означает согласно (2.1), что 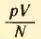одинаково для всех газов в состоянии теплового равновесия.

Конечно, это пока лишь предположение, нуждающееся в экспериментальной проверке. Такую проверку можно произвести, зная V и N всех газов и измеряя их давления при определенной температуре, например при температуре тающего льда.

Так, если 1 моль водорода занимает объем V_H2 = 0,1 м³, то при температуре 0° C его давление оказывается равным p_H2 = 22,65 * 10³ Па. Отсюда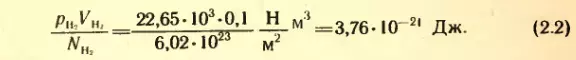

Такое же значение отношения произведения давления газа на его объем к числу молекул получается и для всех других газов при температуре тающего льда. Обозначим это отношение через Θ₀. Тогда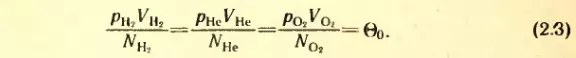

Таким образом, наше предположение оказалось верным.

Правда, соотношение (2.3) не является абсолютно точным. При давлениях в тысячи атмосфер, когда газы становятся весьма плотными, отношение 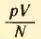перестает быть строго определенным, не зависящим от занимаемых газами объемов. Оно выполняется для достаточно разреженных газов, когда их можно считать идеальными.

Если все сосуды с газами поместить в кипящую при нормальном атмосферном давлении воду (100° C), то 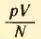= Θ₁₀₀ по-прежнему будет одним и тем же для всех газов, но увеличится. Теперь, как показывает опыт,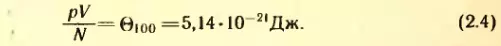

Можно благодаря этому утверждать, что величина Θ зависит от температуры. Более того, Θ ни от чего, кроме температуры, зависеть не может. Ведь Θ не зависит ни от сорта газа, ни от его объема и давления, ни от числа частиц в сосуде, ни от формы самого сосуда.

Определение температуры. Этот опытный факт позволяет рассматривать величину Θ как естественную меру температуры.

В принципе можно было бы считать температурой саму величину Θ и измерять температуру в энергетических единицах – джоулях. Однако, во-первых, это неудобные для практического использования единицы. 100° C соответствовала бы очень малая величина – порядка 10^-21 Дж. А во-вторых, и это главное, уже давно принято измерять температуру в градусах. Будем считать величину Θ прямо пропорциональной температуре T, измеряемой в градусах:

Θ = kT,      (2.5)

где k – коэффициент пропорциональности. Тогда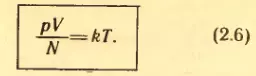

На основании этой формулы устанавливается температурная шкала, не зависящая от выбора вещества, используемого для измерения температуры.