Беседа в венецианском арсенале. Урок физики в VIII классе

Сегодня я расскажу вам кратно о развитии механики.

История не сохранила нам имени того первобытного «инженера-конструктора», которому первому пришла в голову мысль ваять в руки палку, чтобы отвалить тяжелый камень и поймать юркнувшую под него ящерицу. Да и было ли еще имя у этого «инженера»? Я умышленно употребил это звание, потому что слово «инженер» происходит от французского слова «гений», а первая мысль об использовании палки в качестве орудия, увеличивающего силу руки, поистине была гениальной мыслью.

Постепенно, на протяжении многих веков, в практике изготовления орудий охоты, постройки жилищ, а впоследствии городов, в постройке судов, изготовлении орудий труда накапливались опыт и практические умения. Они передавались из поколения в поколение. Конечно, это еще не было наукой. В древних государствах Востока, в Египте зарождающаяся наука была достоянием жрецов, использовавших накопленные знания в корыстных целях. Жрецы были первыми астрономами, ввели летосчисление. Они умели предсказать время разлива Нила и время наступления полевых работ. Для восстановления границ земельных участков, которые ежегодно размывались, приходилось на земле вычерчивать равные фигуры, отсюда ведет свое начало геометрия («землемерие»).

В Греции в отличие от Египта развивающаяся наука не была привилегией жрецов. Греческие ученые были одновременно и философами, и математиками, и естествоиспытателями. Особенным почетом пользовалась у них геометрия. Механика как наука выделилась из геометрии, «Механика» – слово греческое, в переводе на русский язык означает «сложное, затейливое приспособление, хитрую штуку», впоследствии – «мастерство», относящееся к машинам. В настоящее время механика – это наука о простейшей форме движения материи – механическом движении.

В рабовладельческой Греции ремесло, труд, а вместе с ними и физический эксперимент считались делом низким, недостойным свободного гражданина. По словам греческого историка Плутарха, «механика, изгнанная из геометрии, отделилась от нее и долгое время находилась в пренебрежении, став лишь одной из практических отраслей военного искусства». Знаменитый геометр Греции Архимед известен изобретениями многих механизмов и машин: бесконечного винта (рис. 22, а), водоподъемной машины, полиспаста и др. Но тот же историк называет его изобретения «игрушками геометрии». А о том, как пригодились машины Архимеда при защите осажденных римлянами Сиракуз, вы узнаете, прочитав отрывок из сочинения того же Плутарха:

«В это время Архимед и привел в действие свои машины. В неприятельскую пехоту неслись пущенные им различного рода стрелы и невероятной величины камни с шумом и страшной быстротой. Решительно ничто не могло вынести силы их удара, а море внезапно поднимались со стен осажденного города бревна, загнутые наподобие рога. Одни из них ударяли в некоторые корабли сверху и силой удара топили их. Другие железными лапами или клювами, наподобие журавлиных, схватывали корабли за носы, поднимали их в вертикальном направлении на воздух, ставили на корму и затем (удалив крюк) топили».

Живший на сто лет раньше Архимеда греческий философ Аристотель механику определял так: «Под механикой разумеем мы ту часть практического искусства, которая помогает нам разрешать затруднительные вопросы». Познакомимся с одним из таких затруднительных вопросов, известных под названием колесо Аристотеля» (рис. 22, б).

Представим себе колесо, катящееся по прямой линии. Пусть колесо сделает полный оборот. Тогда точка A соприкосновения колеса с прямой коснется прямой в точке A₁ и расстояние |AA₁| будет равно длине окружности колеса. В то же время какая-нибудь другая точка колеса, например точка B, тоже совершит полный оборот, и может показаться, что расстояние |BB₁| равно длине описанной ею окружности. Получается нелепый вывод, что длины окружностей равных радиусов равны между собой. Как согласовать эти развертывания окружностей и перемещения точек? Предлагаем вам, читатель, самостоятельно найти выход из создавшегося затруднения.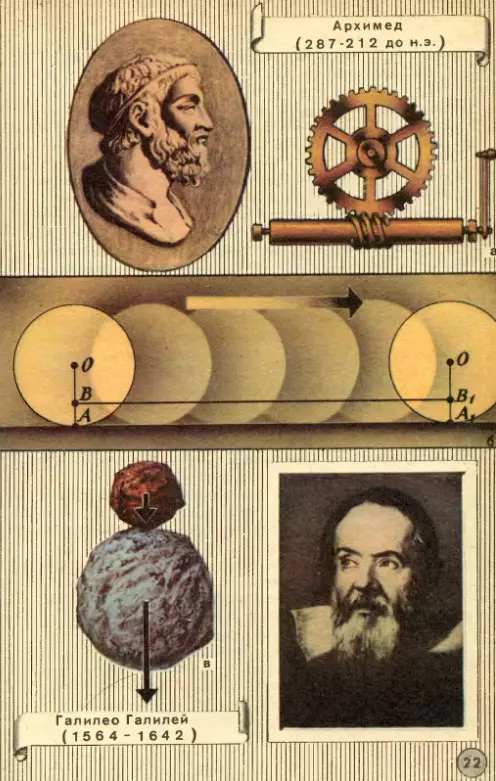

Минуя более чем тысячелетний период средних веков, перенесемся мысленно в Италию, в местечко Арчетри, близ Флоренции, где с 1633 года под надзором инквизиции доживал свои дни Галилео Галилей.

Под страхом отлучения от церкви он вынужден был отречься от учения Коперника о движении Земли. Однако Галилей навсегда остался верным новому мировоззрению. К этому времени он приобрел широкую известность своими открытиями в области механики и астрономии. С помощью сконструированного им телескопа с достаточно большим увеличением он открыл горы на Луне,пятна на Солнце, спутников Юпитера и фазы Венеры. Велика роль Галилея и в развитии механики. Он вполне осознал и применил к решению практических задач закон инерции, хотя и не выразил его с такой четкостью, с какой это сделал позднее Ньютон. Он изучал движение тел под действием силы тяжести: падающих и скатывающихся с наклонной плоскости, качания маятника. В своих выводах он резко разошелся с господствовавшим в то время учением схоластов, придерживавшихся ложного учения Аристотеля. Поскольку учение Аристотеля поддерживалось всесильной тогда католической церковью, то выступление против этого учения считалось опасной ересью.

Чтобы оценить смелость учения Галилея, надо знать эпоху, в которую он жил. Это было триста с лишним лет назад. В Италии еще свежа была память о кровавых правителях Медичи, преступных папах Борджия; в Риме в 1600 году был сожжен живым Джордано Бруно. Во Франции еще не изгладилась память об ужасах варфоломеевской ночи. В Испании и других государствах Европы пылали костры инквизиции, на которых сжигала «колдунов» и «ведьм». В Германии современник и друг Галилея астроном Кеплер едва мог спасти от этой участи свою мать, обвиненную в «колдовстве».

Так вот в эту далекую мрачную пору и жил Галилео Галилей, профессор математики в Падуе, затем во Флоренции, основоположник новой науки, опирающейся не на авторитеты древних писателей, а на опыт, эксперимент. После отречения от учения Коперника, вынужденный удалиться в изгнание, больной, уже слепнущий семидесятилетний Галилей не бросает занятия наукой. В 1638 году в Голландии выходит из печати самое знаменитое из его произведений – «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению».

У меня в руках эта знаменитая книга Галилея (в русском переводе). Книга написана в виде бесед нескольких людей, собирающихся для этой цели в венецианском арсенале (помещении, где хранятся орудия военного назначения).

Главной темой беседы первого дня была «Новая отрасль науки, касающаяся сопротивления твердых тел разрушению».

Прочность твердого тела объясняли тогда боязнью пустоты между отделившимися частями. Галилей боролся с господствовавшим в то время учением и через одного из собеседников проводит мысль, из которой следует, что, несмотря на боязнь пустоты, вода не может быть поднята насосом на высоту, большую 18 локтей (10,33 м). Познакомлю вас кратко еще с одной беседой, в которой говорится о свободном падении тел. Галилей в лице Сагредо и Сальвиати вступает в спор по этому вопросу с Симпличио, сторонником учения Аристотеля.

Симпличио. ...Аристотель доказывает, что существование движения противоречит допущению пустоты. Его доказательство таково. Он рассматривает два случая; один – движение тел различного веса в одинаковой среде; другой – движение одного и того же тела в различных средах. Относительно первого случая и утверждает, что тела различного веса движутся в одной и той же среде с различными скоростями, которые относятся межу собой, как веса тел, так что, например, если одно тело в десять раз тяжелее другого, то и движется оно в десять раз быстрее...

Сальвиати. ...Я сильно сомневаюсь, чтобы Аристотель видел на опыте справедливость того, что два камня, из которых один в десять раз тяжелее другого, начавшие одновременно падать с высоты, предположим, ста локтей, двигались со столь различной скоростью, что, в то время как более тяжелый достиг бы земли, более легкий прошел бы всего десять локтей.

Симпличио. Из ваших слов выходит, что вы производили подобные опыты.

Сагредо. Но я, синьор Симпличио, не производивший никаких опытов, уверяю вас, что пушечное ядро весом в сто, двести и более фунтов не опередит и на одну пядь мушкетную пулю весом меньше полфунта при падении на землю с высоты двухсот локтей.

Сальвиати. И без опытов, путем краткого, но убедительного рассуждения мы можем ясно показать неправильность утверждения, будто тела более тяжелые движутся быстрее, нежели более легкие... В самом деле, скажите мне, синьор Симпличио, признаете ли вы, что каждому падающему твердому телу присуща от природы определенная скорость, увеличить или уменьшить которую возможно только введением новой силы или препятствия?

Симпличио. Я не сомневаюсь в том...

Сальвиати. Таким образом, если мы имеем два падающих тела, естественные скорости которых различны, и соединим движущееся быстрее с движущимся медленнее, как это показано на рисунке, то ясно, что движение тела, падающего быстрее, несколько задержится, а движение другого несколько ускорится. Вы не возражаете против такого положения?

Симпличио. Думаю, что это вполне правильно.

Сальвиати. Но если это так и если вместе с тем верно, что больший камень движется, скажем, со скоростью восемь «градусов», тогда как другой, меньший – со скоростью в четыре «градуса», то, соединяя их вместе, мы должны получить скорость, меньшую восьми «градусов»; однако два камня, соединенные вместе, составляют тело, большее первоначального, которое имеет скорость в восемь «градусов», и, следовательно, выходит, что более тяжелое тело движется с меньшей скоростью, чем более легкое, а это противно вашему предположению.

Симпличио. Я чувствую себя совершенно сбитым с толку. Мне кажется, что малый камень присоединенный к большему, увеличивает вес последнего; но, увеличивая вес, он должен, если не увеличить скорость, то во всяком случае не уменьшить ее.

Сальвиати. Здесь вы совершаете новую ошибку, синьор Симпличио, так как неправильно, что малый камень увеличивает вес большего.

Симпличио. Ну это уже превосходит мое понимание.

Сальвиати. Нисколько, все будет понятно, как только я избавлю вас от заблуждения, в которое вы впали. Дело в том, что необходимо делать различие между телами, пребывающими в покое и находящимися в движении. Большой камень, взвешиваемый на весах, приобретает больший вес от наложения на него не только другого камин: положенная на него связка пакли увеличивает его вес на шесть – десять унций, которые весит сама пакля. Но если вы заставляете камень свободно падать с некоторой высоты вместе с наложенной на него паклей, то думаете ли вы, что при движении пакля будет давить на камень и тем увеличивать скорость его движения или что она его замедлит, поддерживая камень? Мы чувствуем тяжесть на плечах, когда сопротивляемся движению, к которому стремится давящая тяжесть; но если мы опускались бы с такой же скоростью, с какой перемещается свободно падающий груз, то каким образом тяжесть могла бы давить на нас? Не видите ли вы, что это подобно тому, как если бы мы хотели поразить копьем кого-либо, кто бежит впереди нас с равною или большею скоростью? Выведите из этого заключение, что при свободном и естественном падении малый камень не давит на больший и, следовательно, не увеличивает его веса, как то бывает при покое.

Симпличио. Но если положить больший камень на меньший?

Сальвиати. Он увеличил бы вес меньшего, если бы движение его было более быстрым; но мы уже нашли, что если бы меньший двигался медленнее, то он замедлил бы отчасти движение большего. Таким образом, целое двигалось бы медленнее, будучи больше своей части, что противно вашему положению. Выведем из всего этого, что тела большие и малые, имеющие одинаковый удельный вес, движутся с одинаковой скоростью».

«Градус» - старинная мера измерения скорости; в настоящее время не применяется.
Собеседники пользуются старинной единицей измерения массы — унцией; 1 унция ≈ 28,35 г.

Очень интересно и продолжение этой беседы, и все остальные. Любознательным советую ваять в библиотеке «Беседы» Галилея и прочитать их. Там вы найдете много интересных высказываний ученого об ускорения тел, о полете брошенных тел, об ударе и других вопросах механики.

Галилей заложил фундамент современной механики, а о путях ее дальнейшего развития вы узнаете из бесед, в которых мы будем говорить об Исааке Ньютоне.