Тепловое движение

Посмотрите внимательно на следующую таблицу, где показано, как распределяются молекулы азота по скоростям:

Ранее мы приводили для азота значение скорости, равное 454 м/с. Это было среднее значение. В действительности же в газе имеются молекулы с разными скоростями — как выше, так и ниже средней скорости. Иными словами, существует некоторое распределение молекул по скоростям.

Движение отдельной молекулы можно в принципе описать на основе законом механики, если учесть столкновения этой молекулы с другими молекулами и воспользоваться для каждого столкновения законами сохранения энергии и импульса. Правда, чтобы учесть столкновения, надо знать, чему равны координаты и скорости всех молекул газа в от или иной момент времени. При невообразимо огромном числе молекул, имеющихся в любом разумно выбираемом объеме газа, такая программа оказывается заведомо невыполнимой. В применении к большому коллективу молекул законы механики оказываются непригодными. Здесь действуют иные законы — так называемые статистические законы.

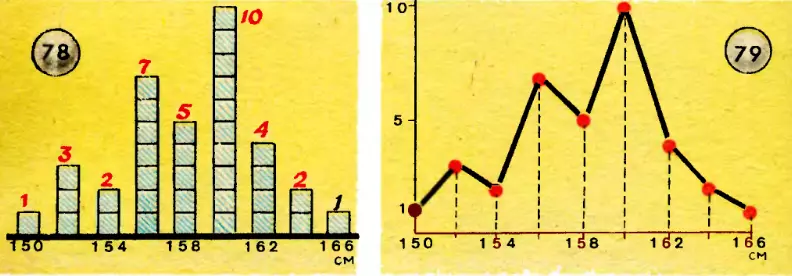
Чтобы получить представление о статистических законах, обратимся к простому примеру. Предположим, что мы измеряем рост учеников в классе. Пусть в классе имеется 35 учеников. При измерении оказалось, что один ученик имеет рост 150 см, трое — 152 см, двое — 154 см, семь — 156 см, пять — 158 см, десять — 160 см, четверо — 162 см, двое — 164 см, один — 166 см. Изобразим результаты измерений в виде диаграммы, заменяя числа учеников с одинаковым ростом столбиками соответствующей высоты (рис. 78). Впрочем, столбики мы могли бы не рисовать. Можно было бы начертить график распределения 35 учащихся по росту (рис. 79). Колебания кривой, как видите, получились большие, и закона распределения еще не чувствуется.

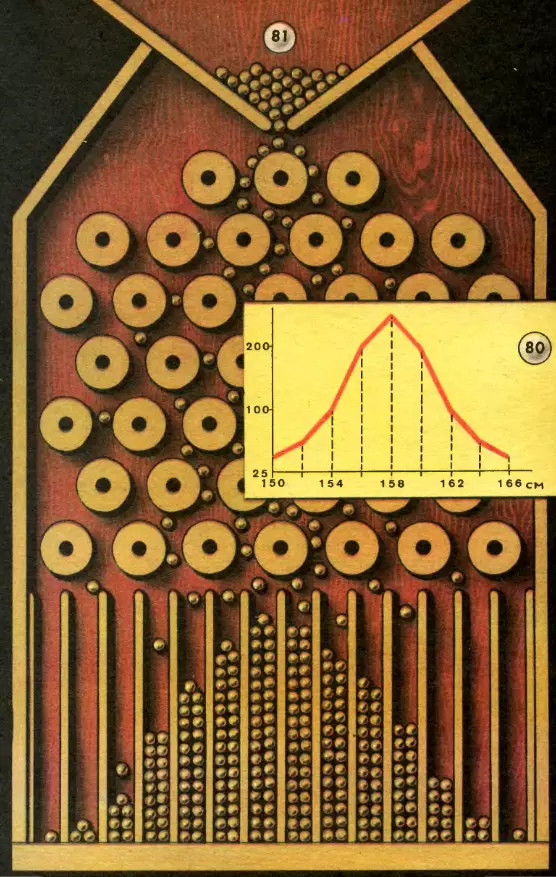
При массовом обследовании учащихся, когда число измерений составит несколько тысяч, на графике получается кривая, которую называют нормальной кривой распределения случайных признаков (рис. 80). По нормальной кривой можно судить о границах роста большинства встречающихся случаев. Определенному классу, т. е. определенной возрастной группе, свойственны определенные границы роста для большинства учащихся. Отклонения от этих границ немногочисленны.

Примерно так же устанавливаются спортивные нормы, например, в беге, стрельбе, прыжках и пр. для каждой возрастной группы учащихся. Чем больше учащихся будет обследовано, тем более плавной получится кривая распределения.

Можно поставить интересный опыт, если смастерить так называемую доску Гальтона. Надо взять широкую ровную и гладкую доску и специальным клеем закрепить на ее поверхности большое число одинаковых деревянных цилиндриков (например, сердцевин от обычных катушек из-под ниток), расположив их так, как показано на рисунке 81. Доску поставим наклонно. Через своеобразную воронку, расположенную в верхней ее части, будем постепенно сыпать дробь (или горох). В нижней части доски укрепим ряд вертикальных перегородок, между которыми будем собираться дробь, скатывающаяся по доске. По краям доски следует прибить невысокие стенки. Каждая дробинка на своем пути от воронки до нижнего края доски испытает ряд столкновений с торчащими на поверхности доски цилиндриками. Цилиндрики размещены по поверхности доски так, что всякий раз дробинке равновероятно скатиться как с левого, так и с правого края цилиндрика. Накопившиеся между перегородками дробинки (при достаточно большом их количестве) наглядно демонстрируют нормальную кривую распределения (см. рисунок).

В мире молекул распределение скоростей подчиняется определенному закону. Нельзя говорить о температуре или давлении одной или небольшого числа (5, 10 или 100) молекул. Движение одной какой-нибудь молекулы не характеризует свойств газа. Законы тепловых движений не могут быть сведены к законам механики. Тепловое движение представляет собой более сложную форму движения по сравнению с механическим перемещением. Массовость и случайность являются основными условиями для применения статистических законов. Поэтому мы не можем, например, сказать, сколько молекул данного газа в данный момент имеет скорость 454 м/с, но мы можем говорить, что, вероятно, встретим в данном объеме газа при данной температуре определенный процент молекул, скорость которых лежит в пределах, скажем, от 400 до 500 м/с.

Обозначим через Δn(v) число молекул в единице объема, скорости которых попадают в интервал значения от v до v + Δv. При достаточно малых Δv можно считать, что

Δn(v) = F(v)Δv.

Вид функции F(v) был установлен великим английским физиком Максвеллом:

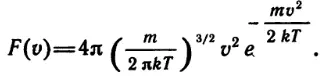
Здесь m — масса молекулы, k — постоянная Больцмана, T — абсолютная температура газа. График функции F(v) (знаменитое распределение Максвелла) показан на рисунке 82. При достаточно малых значениях скорости эта функция ведет себя как парабола av²; при больших скоростях она ведет себя как экспоненциальная функция 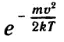. Средняя скорость молекулы примерно соответствует той скорости, при которой функция F(v) принимает наибольшее значение.

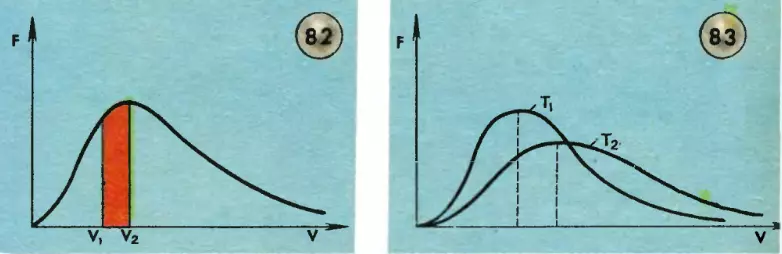
Выберем два значения скорости: v₁ и v₂. Доля молекул, имеющих скорости в интервале значений от v₁ до v₂, равна отношению закрашенной на рисунке площади ко всей площади под кривой F(v).

Молекулы сталкиваются друг с другом; их скорости все время изменяются не только по направлению, но и по модулю. Тем не менее число молекул в некотором выбранном интервале значений скорости остается практически неизменным. Иными словами, показанное на рисунке 82 распределение оказывается постоянным во времени. Чтобы изменить его, надо изменить температуру газа.

На рисунке 83 показаны два распределения Максвелла — одно при температуре T₁, другое при температуре T₂, причем T₂ > T₁. Видно, что с повышением температуры максимум распределения смещается в сторону более высоких скоростей. Это означает, в частности, что с повышением температуры увеличивается среднее значение скорости молекулы.

Статистические законы распределения применяются в науке, в различных отраслях хозяйства, экономической жизни, вопросах страхования и т. д.