Четыре затруднительных положения
Движенья нет, сказал мудрец брадатый.
Другой смолчал и стал пред ним ходить.
Сильнее бы не мог он возразить;
Хвалили все ответ замысловатый,
Но, господа, забавный случай сей
Другой пример на память мне приводит:
Ведь каждый день пред нами солнце ходит,
Однако ж прав упрямый Галилей.
(А. С. Пушкин.)
«Забавный случай» этот, если верить легенде, произошел в небольшом древнегреческом городке Элее (на юге Италии). Лет за 500 до нашей эры жил здесь знаменитый философ Зенон. К Зенону из разных мест стекались юноши и взрослые мужи приобщиться его мудрости. «Я (Сократ) могу тебе назвать Пафодора, сына Иссолоха, и Каллия, сына Каллиана, которые оба стали мудрыми и славными благодаря общению с Зеноном, за что заплатили ему по сто мин каждый».
Странным показалось бы учение Зенона в наши дни. Он отрицал возможность познания мира посредством наших чувств: «верить можно только разуму». Мир, по его учению, неизменен и неподвижен. Несмотря на свидетельства наших чувств, утверждал он, нельзя разумом доказать существование движения в мире. Излюбленным приемом доказательства своих слов Зенон избрал доказательство от противного, приведение к абсурду (нелепости). Первая из его знаменитых апорий (греч. «безвыходное положение, тупик, непреодолимые трудности») именно и имела целью доказать невозможность движения. «Движенья нет...», оно даже не может начаться. Чтобы пройти расстояние AB (рис. 19, а), надо сначала пройти половину его, AB1, а еще раньше надо пройти одну четвертую часть, AB2, и т. д. Продолжая делить пополам все уменьшающиеся отрезки, мы никогда не кончим деления и, следовательно, никогда не начнем движения.
Возмущенный такими словами, другой мудрец встал и вышел из помещения; практика – вернейшая проверка теории.
Ошибка Зенона ясна: из возможности бесконечного деления отрезка он неправомерно делал вывод о бесконечности времени, требуемого для прохождения отрезка.
Вторая апория Зенона – «Ахиллес и черепаха» – представляет собой почти повторение первой, но выражена в столь оригинальной форме, что если вы предложите эту задачу вашим товарищам в классе, то наверняка возникнут горячие споры. Вот эта задача: быстроногий Ахиллес (герой троянской войны) никогда не догонит черепаху, хотя последняя, как известно, считается образцом медленности движения. Пока Ахиллес проходит расстояние, разделявшее их первоначально, черепаха не ждет, а продолжает ползти, и Ахиллесу надо пройти первоначальное расстояние плюс образовавшееся новое расстояние (рис. 19, б). Но когда Ахиллес пройдет и новое расстояние, черепаха, продолжая ползти, опять уйдет от Ахиллеса, и последнему опять надо будет догонять черепаху, и так можно продолжать рассуждение бесконечно долго. Получается, что Ахиллесу никогда не настичь черепахи.
Но ведь это неправда! Вы легко опровергнете этот парадокс, если знаете формулу равномерного движения и умеете решать уравнение с одним неизвестным. Конечно, Ахиллес догонит черепаху. Пусть это произойдет через какое-то время t. За это время он пройдет расстояние, измеряемое произведением vAt, где vA – скорость Ахиллеса. Черепаха за то же время проползет расстояние, измеряемое произведением vЧt, где vЧ – скорость черепахи. Если первоначальное расстояние, отделявшее Ахиллеса от черепахи, обозначить d, то можно написать:
vАt = vЧt + d.
Отсюда находим:
t = d / (vА – vЧ).
Можно решить эту задачу иначе. Скорость Ахиллеса vА больше скорости черепахи vЧ, поэтому расстояние между ними сокращается за единицу времени на vА – vЧ. Все расстояние между Ахиллесом и черепахой обозначим d, оно будет пройдено за время t = d / (vА – vЧ). За это время Ахиллес и догонит черепаху.
Третья апория – «Стрела». Она интересна тем, что раскрывает важнейшее свойство движения – его относительность. Но сначала послушаем Зенона. Выпущенная из лука стрела (рис. 19, в) в какой-то момент времени находится в точке А. В это мгновение она покоится. Когда стрела достигнет точки В, то можно будет утверждать, что она покоится в этот момент в этой точке В. В какой бы точке мы ее ни застали, она покоится в тот момент, в который находится в этой точке, т. е. покоится в любой момент, покоится вообще.
В чем же тут дело? Зенон, очевидно, смешивал точку на стреле с точкой вне стрелы. Да, конечно, стрела неподвижна относительно точки А, взятой на самой стреле, как неподвижны друг относительно друга предметы в вагоне движущегося поезда.
Обитатели Земли охотно считают Землю неподвижной; она действительно неподвижна относительно находящихся на ней предметов. Но Земля мчится вокруг Солнца, одновременно вращаясь вокруг своей оси. Об этом и думал «упрямый Галилей», когда, согласно преданию, после своего отречения от «ереси вращения Земли» воскликнул: «А все-таки она движется».
Вот четвертая из известных апорий Зенона против движения, называемая «Стадион», по-гречески – «ристалище, бега» (рис. 19, г). Представьте себе три параллельных ряда всадников, готовых к старту. Сигнал! Второй ряд мчится направо, третий – с той же скоростью налево, а первый ряд остается на месте. К некоторому моменту времени всадник второго ряда промчался на половину неподвижного ряда, т. е. на s/2. Но за то же время он ускакал от замыкающего всадника третьего ряда на целый ряд, т. е. на s. Так как за одинаковые промежутки времени всадник должен проскакать одинаковые расстояния, то s/2 = s. Поскольку это нелепо, то получается, что движение само себя отрицает.
Наивно? Да, наивно. Теперь каждый школьник, немного знакомый с физикой, скажет, что если скорость всадника второго ряда относительно первого, неподвижного ряда равна v, то относительно третьего ряда, движущегося в том же аллюре, она равна 2v и перемещение относительно движущегося ряда вдвое больше, чем относительно неподвижного. Не будем, однако, очень строги к Зенону. Во-первых, это было почти две с половиной тысячи лет назад, а во-вторых, мы должны оценить заслугу Зенона, который одним из первых указал на противоречивость движения. Однако, не сумев объяснить эту противоречивость, он пришел к «опровержению» движения.
В жизни нам не раз приходится сталкиваться с относительным характером движения и становиться жертвой не всегда легко разрешимых иллюзий (обмана чувств). Не приходилось ли вам из окна движущегося поезда наблюдать движение другого поезда, идущего по параллельному пути? В какое-то время этот поезд обгоняет ваш. Но вот машинист, словно угадав ваше желание, прибавляет ход, и вы торжествуете: скорость вашего «соперника» становится все меньше и меньше, вот уже оба поезда кажутся неподвижными относительно друг друга, и, наконец, «ура», обогнали! Вагоны соседнего поезда «уплывают» назад! Вся эта сценка – результат относительности скоростей.
Насколько различными оказываются движения тела, если их рассматривать относительно различных, как говорят, тел отсчета, убедительно покажет вам пример колеса, катящегося по ровной поверхности (рис. 20). Как вы думаете, какова траектория какой-нибудь точки катящегося колеса, например точки А? Вопрос не имеет смысла, скажете вы, если не указать систему отсчета. Относительно поверхности земли траектория точки А – циклоида. Отметим попутно, что по этой кривой вычерчивают профиль некоторых зубчатых колес, когда хотят добиться плавного качения зуба по зубу в передаче. Относительно движущегося экипажа точка А описывает окружность.
Приведем еще один пример.
Каждый из вас наблюдал наклонные струйки дождя на оконном стекле движущегося вагона. А для «неподвижного» наблюдателя, стоящего на платформе, капли дождя в безветренную погоду падают вертикально.
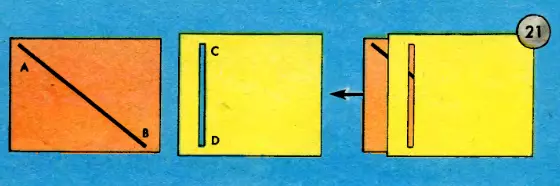
Вы можете сделать простой прибор, хорошо поясняющий это наблюдение. Вырежьте два прямоугольника из плотной бумаги. На одном проведите жирную наклонную черту АВ (рис. 21), изображающую след капли на стекле движущегося вагона. На другом листке сделайте вертикальный прорез CD. Наложите второй листок на первый. Тяните теперь нижний листок из-под верхнего в направлении движения вагона. Вы увидите в прорез перемещающуюся черную точку (каплю).
Так и для наблюдателя, стоящего неподвижно вне вагона, капля движется вертикально вниз, а для наблюдателя, движущегося вместе с вагоном, капля движется по наклонной линии АВ.