Необходимое дополнение о средней скорости
В двух предыдущих беседах вы несколько раз встречали выражение «средняя скорость». Считаю необходимым дать разъяснение атому понятию, так как оно не всегда правильно освещается в книгах по физике. Так, некоторые авторы утверждают, что средняя скорость (как и всякая скорость) есть величина векторная и имеет направление от начальной точки к конечной точке перемещения. Другие же, наоборот, рассматривают среднюю скорость как отношение пройденного пути ко времени и потому считают среднюю скорость скаляром.
Какое же утверждение верно: средняя скорость – скаляр или вектор? Ответ зависит от определения средней скорости. Если ее определять как скорость перемещения, т. е. как отношение перемещения ко времени, за которое это перемещение произошло, средняя скорость будет вектором. Ведь перемещение есть вектор. Если же средняя скорость определяется как отношение пройденного пути (длины траектории) ко времени, то она будет скалярной величиной.
Допустим, вы ждете к себе двух товарищей, выезжающих в одно время из одного и того же места. Первый приехал к вам через час после выезда, тогда как второй, допустим, явился через 2 ч. Вы, естественно, бросаете ему упрек: «Как медленно ты ехал!» Ваше возмущение понятно: ведь расстояние до вас от места отправления обоих товарищей одно и то же, например 60 км. Простой расчет показывает, что средняя скорость первого была 60 км/ч, второго 30 км/ч. Транспортные средства (автомобиль) одни и те же. В чем же дело? Оправдание: «Да я же заезжал в C, в D и в E».
Скорости 60 и 30 км/ч – скорости перемещения, величины векторные, направленные от A к B (рис. 17, а). Но второй товарищ не согласен с таким определением его скорости. Спидометр на его машине показывал то же, что и на машине первого (60 км/ч). Что же измерял спидометр? Он измерял скорость движения по траектории ACDEB. Скорость могла в отдельные моменты меняться. Это мгновенная скорость, величина векторная, направленная по касательной к траектории (рис. 17, б). После пробега некоторого участка или всего маршрутного пути можно найти среднюю скорость на участке, взяв отношение длины пути (не перемещения) ко времени. Это уже средняя скорость движения по траектории, величина скалярная.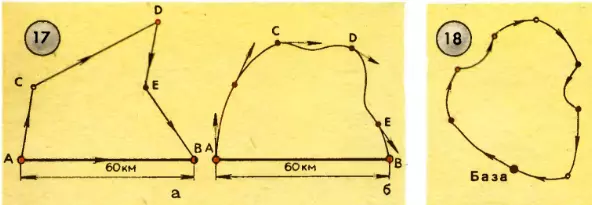
Рассмотрим еще пример. Шофер, выехавший с базы (рис. 18) по путевке с объездом различных пунктов, вернулся снова на базу через 6 ч. Пусть длина пройденного машиной пути равна 120 км. Определение средней скорости как скорости перемещения в этом случае не годится. Перемещение равно нулю, машина вернулась в исходную точку. Но ведь бензин израсходован, единственное объяснение этого расхода – работа двигателя машины на пути 120 км при скорости 120 км / 6 ч = 20 км/ч. Эта средняя скорость – скаляр.
Итак, различайте среднюю скорость перемещения (величина векторная) и среднюю скорость движения на участке траектории (скаляр).
А если вы захотите немного отвлечься от физики, прочтите книгу Жюля Верна «Путешествие вокруг света в 80 дней» и проведите диспут с товарищами, о какой скорости там говорится на различных участках, которые проехал Филеас Фогт на поезде, на пароходе, на слоне, на парусной лодке и в целом на всем пути. Возникнет много вопросов, и спор принесет пользу его участникам.
