Маятник

Всюду в нашей жизни мы встречаемся с колебательными движениями, начиная от качаний маятника, колебаний рессор и сотрясений кузова автомобиля или вагона поезда до страшных, разрушительных колебаний коры нашей планеты. Фабричные трубы и высокие здания колеблются под действием ветра, подобно полотну ножовки, зажатому одним концом в тисках. Правда, такие колебания не так уж велики. Амплитуда колебаний вершины Эйфелевой башни в Париже (высотой 300 м) при сильном ветре около 50 см.

Колебания! Наш взгляд падает на маятник стенных часов. Неугомонно спешит он то в одну, то в другую сторону, своими ударами как бы разбивая поток времени на точно размеренные отрезки. «Раз-два, раз-два», - невольно повторяем мы в такт его тиканью. Качание влево и обратно вправо, в исходное положение, составляет полное колебание маятника, а время одного полного колебания называют периодом колебания. Число колебаний тела в секунду называется частотой колебания.

Изучение колебаний начинается с изучения движения простого нитяного маятника, который вы легко можете изготовить, подвесив небольшой металлический шарик на нитку. Уменьшая мысленно размеры шарика до материальной точки, а нити приписывая идеальные свойства: невесомость, абсолютную гибкость и отсутствие трения, мы придаем к теоретическому, так называемому «математическому маятнику».

Период колебания маятника выражается формулой 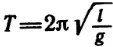, где l — длина маятника, g — ускорение свободного падения. Ни масса маятника, ни угол отклонения от положения равновесия в эту формулу не входят, так как период колебания маятника от них не зависит.

Как объяснить движение маятника, которые повторяются с одним и тем же периодом и могли бы продолжаться вечно, если бы маятник не встречал сопротивления движению в виде трения и не совершал бы работы, преодолевая это сопротивление? Очевидно, движение маятника происходит за счет сообщения ему энергии. Когда мы отводим маятник от вертикального положения, то сообщаем ему некоторый запас потенциальной энергии. Когда маятник опускается из точки B в точку A (рис. 60, а), потенциальная энергия, запасенная при подъеме переходит в кинетическую. Скорость маятника увеличивается, но не равномерно, потому что сила, сообщающая ускорение, уменьшается. В точке A скорость маятника будет наибольшей, поэтому маятник не может остановиться в этой точке, вследствие инерции он будет продолжать движение. Поскольку шарик привязан к нити, то подниматься в точку C он будет по дуге окружности. Высота подъема равна высоте опускания маятника. Это подметил еще Галилей в своем опыте, известном под названием «маятник Галилея» (рис. 60, б). Вбив по одной вертикальной линии, проходящей через положение равновесия маятника, гвоздики на различной высоте и пуская маятник, он подметил, что, обогнув гвоздик, маятник поднимался вправо на такую же высоту, с какой был опущен.

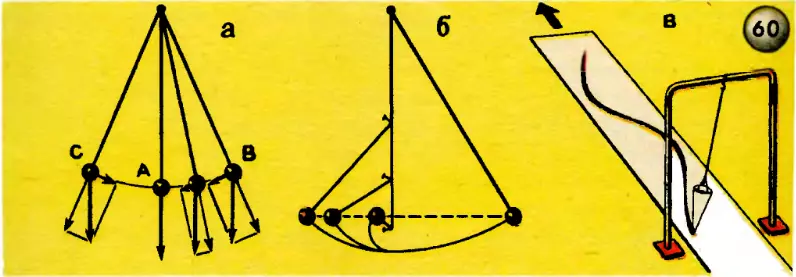
Колебания маятника — пример на закон сохранения энергии.

Колебания маятника — это гармонические колебания.

Что такое гармонические колебания, попробуем выяснить на опыте.

Подвесим воронку, склеенную из плотной бумаги и наполненную сухим, просеянным через частое сито песком, как показано на рисунке 60, в. Под воронку положим длинную полосу картона, выкрашенного в белый цвет. Пустив воронку качаться, как маятник, будем двигать картонную полоску равномерно в направлении, перпендикулярном к плоскости качания маятника. Высыпающийся из воронки песок «запишет» на картоне волнообразную линию, называемую синусоидой. Колебания, происходящие по закону синуса, называются синусоидальными или гармоническими. Происхождение слова «гармонический» уходит в даль веков, в историю Древней Греции, к учению Пифагора, искавшего начало всех начал в числах и учившего, что порядок и красота Вселенной основаны на числах.

Рассмотрев внимательно синусоиду, образованную на картоне, вы заметите, что песок ложится неодинаковой толщиной: чем ближе к вершине или впадине синусоиды, тем гуще насыпан песок. Это свидетельствует о том, что скорость маятника в этих точках была меньше, обращаясь в нуль в самых верхних и самых нижних точках кривой, т. е. в точках, где маятник менял свое движение на обратное. Среднее положение маятник проходил с максимальной, накопленной во время падения скоростью и потому оставлял тонкий след.

Большое значение при изучении колебательных процессов имеет понятие «фаза».

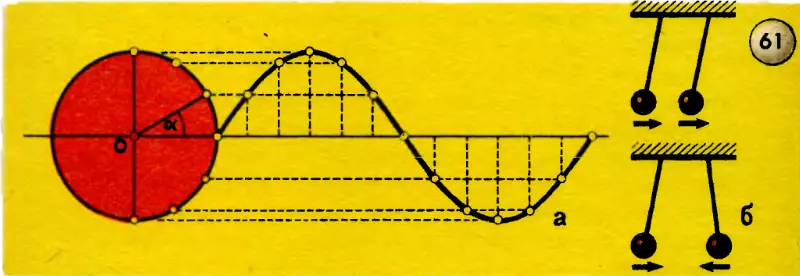
Фаза — слово греческое, в переводе на русский язык означает «проявление». В физике этим словом характеризуют стадию (ступень) развития периодического процесса, например: начало его, максимум развития, минимум и т. д. Однако такого определения фазы, как физической величины, недостаточно. Надо знать, как ее можно измерить. Для этого рассмотрим прием графического построения синусоиды (рис. 61, а). Из точки O как из центра опишем окружность и на продолжении горизонтального диаметра проведем горизонтальную линию (ось синусоиды). Представим, что по этой окружности равномерно вращается точка. Проекция радиуса-вектора, проходящего через последовательные положения точки, дадут нам значения соответствующих ординат точки синусоиды, а угол поворота радиуса вектора при этом, считая от горизонтальной оси против часовой стрелки, будет характеризовать положение точки на окружности, т. е. характеризовать стадию развития процесса. Этот угол называется фазовым углом или просто фазой. На рисунке 61, б показаны два маятника: вверху в одинаковых фазах, внизу в противоположных фазах колебания.

Маятник или другая колебательная система, приведенная в движение и предоставленная самой себе, совершает, как говорят, свободные колебания.

Предоставленный самому себе маятник будет продолжать качаться, но размахи его, амплитуды колебания, будут становиться все меньше и меньше, колебания будут затухать. Движение колеблющегося маятника переменное: то ускоренное, то замедленное, но это движение и не равномерно переменное. Как видно из чертежа, сила, сообщающая маятнику ускорение, уменьшается по мере уменьшения угла отклонения маятника от вертикального положения. В пружинном маятнике сила упругости растянутой или сжатой пружины непостоянна и сообщаемые маятнику ускорения тоже непостоянны. Такая зависимость ускоряющей силы от расстояния колеблющейся точки до положения равновесия является основным признаком гармонического движения. Гармоническими колебаниями называют поэтому колебания, вызванные силой, возрастающей пропорционально отклонению от положения равновесия. Колебания маятника можно считать гармоническими лишь при небольших отклонениях маятника от положения равновесия, не больших 10°.

В практике часто бывает необходимо поддержать колебания, не давать им затухать. Ясно, что для этого придется подводить к колеблющемуся телу энергию извне. В тех случаях, когда система приводится в колебательное движение действием какой-нибудь внешней, изменяющейся по модулю силы, мы будем иметь дело не со свободными, а с вынужденными колебаниями. Такие колебания, навязанные системе извне, будут происходить с частотой изменения силы, вызывающей эти колебания. Например, колебания фундамента двигателя являются вынужденными и происходят с частотой колебаний двигателя.

Непериодические изменения внешней силы, конечно, отражаются на частоте колебаний. Так, записанная на граммофонной пластинке речь или музыка повторятся мембраной патефона, приходящей в колебания с меняющейся частотой, а значит, воспроизводящей звуки различной высоты и громкости. Эти колебания вызваны толчками, которые получает иголка, двигаясь по дорожке звукозаписи. Если у вас есть граммофонная пластинка, то вы можете воспроизвести записанную на пластинке музыку или речь, приставив к равномерно вращающейся пластинке открытку или листок плотной бумаги.

В том случае, когда частота изменения внешней силы совпадает с собственной частотой колебательной системы, происходит увеличение амплитуды колебаний этой системы. Так, периодически подталкивая качели, в такт их собственным колебаниям, мы можем очень сильно раскачать их. Такое явление носит название резонанса и имеет огромное значение в технике. Настраивая радиоприемник на определенную частоту, вы приводите его в резонанс с радиовещательной станцией.

Опасные последствия, которые могут быть вызваны резонансом (разрушение мостов, потолочных перекрытий, фундаментов), описаны в любом учебнике физики.

Остановимся еще на одном виде колебаний — автоколебаниях. Так называются колебания, происходящие с собственной частотой колеблющейся системы, но под действием не переменной, а постоянной силы. Когда скрипач равномерно ведет смычок по струне скрипки, струна совершает собственные автоколебания, дающие звук определенного тона. Когда анкер часов своими палетами (зубьями) соприкасается с зубьями ходового колеса, они подталкивают их в направлении движения. В результате маятник колеблется с собственной частотой, зависящей только от его длины.