Физика космических полетов

Но вернемся к физике. Я коснусь лишь элементарных сведений о физике космических полетов. Даже если некоторые расчеты покажутся вам трудными, я рекомендую терпеливо взобраться в них, так как они помогут вам лучше понять финку, а ведь это главная цель данной книги.

Из школьного курса вы знаете, какую траекторию имеет тело, брошенное горизонтально над поверхностью Земли. Движение такого тела, например камня, слагается из движения в горизонтальном направлении с начальной скоростью и движения вертикально вниз по законам свободного падения. Камень приближается к Земле, и проходимые им в этом направлении пути а 1, 2, 3 с и т. д. относятся как квадраты этих чисел (1:4:9 т. д.). В результате сложения этих двух движений получается траектория, называемая параболой. Можно подумать, что продолжительность полета зависит от скорости, с которой брошен камень. Однако это не так.

Один взгляд на рисунок 50, а покажет вам, что камень, брошенный с вдвое большей скоростью, пролетит вдвое большее расстояние; время же полета в обоих случаях будет одинаковым. При небольшой начальной скорости движения тела поверхность Земли можно принимать за горизонтальную. Для шарообразной Земли продолжительность полета, конечно, зависит от начальной скорости, и при некоторой (очень большой) скорости брошенное горизонтально тело может вообще не упасть на Землю, станет описывать круговые траектории, оставаясь на одной и ой же высоте над поверхностью Земли. Это случится, когда ускорение, сообщаемое телу силой тяжести, будет равно центростремительному ускорению, соответствующему данной скорости тела на круговой орбите: 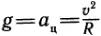, где R – радиус орбиты. Из приведенного равенства для данного случая можно найти модуль необходимой скорости:

Принимая R равным радиусу Земли (6400 км), получим: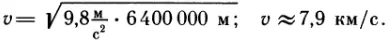

Следовательно, тело, «брошенное» горизонтально с такой скоростью, не упадет на землю, а будет описывать круговые траектории. Эту скорость называют первой космической скоростью.

Представим себе, что из некоторой точки над поверхностью Земли запускаются по касательной к этой поверхности тела с разной начальной скоростью (рис. 50, б). При скорости 7,9 км/с, как мы уже видели, тело не падает на Землю, а становится ее спутником, двигаясь вокруг нее по круговой орбите. При скорости выше 7,9 км/с орбита спутника становится эллиптической. При скорости 11,2 км/с (вторая космическая скорость) тело движется по кривой, близкой к параболе; оно выходит за пределы земного притяжения и превращается в искусственную планету Солнечной системы.

Ракета обычно запускается вертикально, затем на соответствующей высоте по заданной программе поворачивается на некоторый угол к вертикали и по прекращении работы двигателя выводимый ею аппарат движется свободно по эллиптической траектории, в дальнем фокусе эллипса находится центр Земли. При достаточно большой начальной скорости (большей 7,9 км/с) космический аппарат не возвращается на Землю, а становится спутником нашей планеты. Двигаясь по эллиптической орбите, спутник находится в поле земного тяготения.

Познакомимся с элементарным выводом формулы скорости, необходимой для того, чтобы ракета перешла на бесконечную параболическую траекторию и, следовательно, улетела из поля земного тяготения в мировое пространство. Тело, поднятое над Землей, обладает потенциальной энергией, определяемой работой, совершенной при его поднятии. На расстоянии в несколько тысяч километров от Земли сила притяжения тел к Земле заметно уменьшается.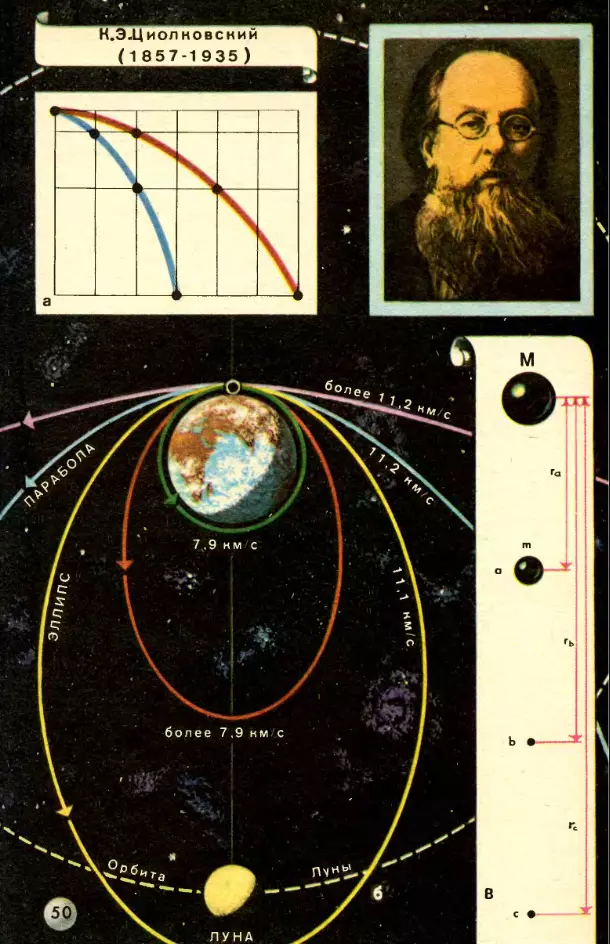

Подсчитаем, например, работу, необходимую для перенесения тела массой m из точки a в точку c (рис. 50, в). Масса другого тела M.

По закону всемирного тяготения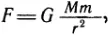

где G – гравитационная постоянная. Мы видим, что сила зависит от расстояния r между рассматриваемыми телами. Иначе говоря, сила F непостоянна: по мере перенесения тела массой m из точки a в точку c сила уменьшается. Это необходимо принимать во внимание при подсчете работы.

Разделим расстояние ac на несколько участков (для простоты разделим на два участка: ab и bc) и подсчитаем работу, произведенную на каждом участке отдельно. В точке a сила притяжения равна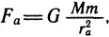

а в точке b она равна: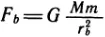

Для вычисления работы определим среднее значение силы. Но какое среднее значение определить: среднее арифметическое, равное полусумме крайних значений, или среднее геометрическое, равное корню квадратному из произведения этих значений? Точно подсчитать работу переменной силы можно только средствами высшей математики, которая подтвердила, что правильным является выбор среднего геометрического, а не среднего арифметического.

Итак, средняя сила на участке ab.

Как велика работа для перенесения тела массой m из точки a не в точку c, а в бесконечность? Ученик, который сказал бы, что для удаления тела в бесконечность нужно совершить бесконечно большую работу, оказался бы неправ. В самом деле, если 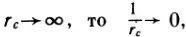, поэтому работа для удаления тела из данной точки в бесконечность имеет вполне конечное значение: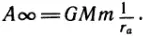

Минимальная начальная скорость, при которой тело массой m способно уйти бесконечно далеко от тела массой M, получила название скорости убегания или ускользания. Она может быть вычислена на основе закона сохранения энергии. Работа для удаления тела в бесконечность, очевидно, совершается за счет кинетической энергии 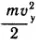, сообщенной при запуске телу массой m:

Именно с такой или несколько большей скоростью были отправлены космические ракеты, которые вырвались на плена тяготения Земли и превратились в спутники Солнца. Конечно, vy – это скорость при запуске. Выйдя на орбиту вокруг Солнца, ракета движется со скоростью Земли. Она имела эту скорость еще будучи на Земле.

Все вышеприведенные рассуждения относились к телу, масса которого остается неизменной. В действительности же масса ракеты, по мере того как сгорает топливо, уменьшается. Движение тела с переменной массой рассматривалось в конце XIX столетия русскими исследователями К. Э. Циолковским и И. В. Мещерским.

Приведем без доказательства формулу Циолковского для определения максимальной скорости, которую получит ракета по израсходовании топлива: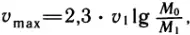

где v₁ – скорость истечения газов, M₀ – масса ракеты в момент старта с полным запасом топлива, M₁ – масса ракеты после израсходования топлива. Отношение 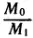получило название числа Циолковского. Для читателей, знакомых с логарифмами, интересно будет подсчитать это отношение при скорости истечения газов 2,5 км/с: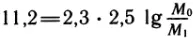

Отсюда получается, что 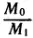= 88, т. е. масса ракеты с топливом должна в 88 раз превосходить массу самой ракеты! Ясно, что по конструктивным соображениям построить такую ракету практически невозможно. Если увеличить вдвое скорость истечения газов, то отношение 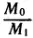уменьшится до 10. Такую ракету построить уже можно.

Но есть и другой путь увеличения скорости ракеты, указанный тоже Циолковским, – создание многоступенчатых ракет. По мере отработки ступени она отделяется от ракеты. Тогда вступает в действие следующая ступень.
Современная космонавтика использует именно составные ракеты (напомним читателю рис. 47, в).