Скорость при прямолинейном равноускоренном движении
При движении реального тела, например едущего из Москвы в Санкт-Петербург автомобиля, его ускорение может все время изменяться. При этом зависимость ускорения автомобиля от времени может быть достаточно сложной. Мы начнем изучение ускоренного движения с самого простого его вида – прямолинейного равноускоренного движения.
Прямолинейное движение тела называют равноускоренным, если в процессе движения значение ускорения остается постоянным, т. е. не изменяется с течением времени.
Если значение a ускорения движущегося тела постоянно, и мы знаем начальную скорость этого тела v0, то можно найти скорость тела vк в любой последующий момент времени t. Будем для упрощения дальнейших вычислений считать (так обычно и делают), что t0 = 0. Тогда Δt = t - t0 = t. Поскольку мы рассматриваем лишь случай прямолинейного движения тел вдоль оси X, то по определению значение ускорения вдоль этой оси
a = (vк - v0) / Δt = (vк - v0) / t.
Тогда vк - v0 = a · t, поэтому vк = v0 + a · t.
В полученном выражении vк – значение скорости вдоль оси X в момент времени t.
Это выражение называют зависимостью значения скорости от времени при прямолинейном равноускоренном движении. Обратим еще раз внимание на то, что начальный момент времени в этом выражении мы полагали равным нулю.
Зависимость значения скорости от времени при прямолинейном равноускоренном движении имеет вид:
v = v0 + a · t.
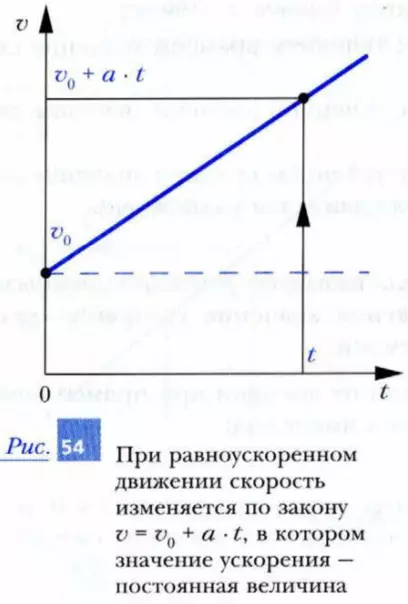
Если изобразить эту зависимость графически, то мы получим прямую линию (рис. 54). Из графика видно, что в момент t0 = 0 значение скорости равно v0. При увеличении времени на t значение скорости возрастает до величины v0 + a · t.
Рассмотрим пример равноускоренного движения.
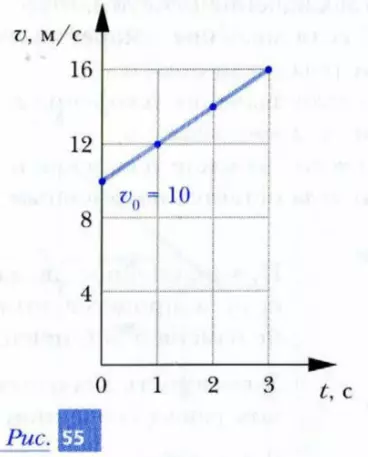
Пусть водитель автомобиля, который движется в положительном направлении оси X со скоростью, имеющей значение v0 = 10 м/с в момент t = 0, нажимает на педаль газа. В результате автомобиль начинает разгоняться с постоянным ускорением, имеющим значение a = 2 м/с2. Опишем изменение скорости автомобиля аналитическим, табличным и графическим способами. Так как значение ускорения автомобиля a = 2 м/с2, то значение его скорости за каждую секунду будет увеличиваться на 2 м/с. Следовательно, в момент времени t = 1 с оно будет равно
v1 = 10 + 2 · 1 = 12 (м/с).
К моменту t = 2 с, т, е. через 2 секунды после начала равноускоренного движения,
v2 = 10 + 2 · 2 = 14 (м/с),
через 3 секунды –
v3 = 10 + 2 · 3 = 16 (м/с) и т. д.
Таким образом, через t секунд значение скорости будет равно
v = 10 + 2 · t = v0 + a · t.
Полученные результаты приведены в таблице и на рис. 55.

В заключение отметим, что:
1) если значение ускорения a > 0, то с течением времени значение скорости тела увеличивается;
2) если значение ускорения a < 0, то с течением времени значение скорости тела уменьшается;
3) если значение ускорения a = 0, то с течением времени значение скорости тела остается неизменным, т. е. тело движется равномерно.
Итоги
Прямолинейное движение тела называют равноускоренным, если в процессе этого движения значение ускорения тела не изменяется с течением времени. Зависимость значения скорости от времени при прямолинейном равноускоренном движении имеет вид:
v = v0 + a · t,
где v0 – значение скорости тела в момент времени t = 0, a – значение постоянного ускорения тела, v – значение скорости тела в момент времени t.
Вопросы
- Какое прямолинейное движение тела называют равноускоренным?
- Выведите зависимость значения скорости от времени при прямолинейном равноускоренном движении.
- Как изменяется значение скорости во времени при равноускоренном движении, если: а) a > 0; б) a < 0; в) a = 0?
Упражнения
1. Значение ускорения автомобиля при прямолинейном равноускоренном движении было равно a = 2 м/с2 в течение промежутка времени Δt = 4 с. В конце этого промежутка времени автомобиль двигался в положительном направлении оси X со скоростью, значение которой стало равным vк = 10 м/с. Найдите значение скорости этого автомобиля в момент времени, соответствующий началу данного промежутка времени. Предварительно ответьте на вопрос разгонялся или тормозил автомобиль в течение этого промежутка времени?
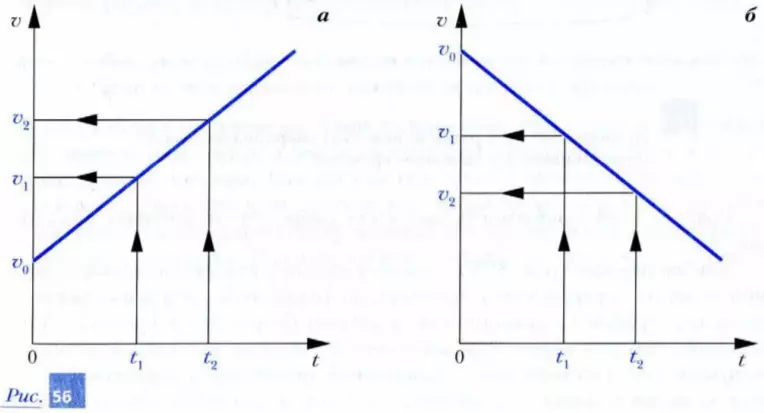
2. На рис. 56 изображены графики зависимости значения скорости от времени для двух точечных тел. Напишите выражения для расчета значений ускорений этих тел. В каком из представленных случаев значение ускорения положительно?