Прямолинейное равномерное движение

Изучение прямолинейного движения мы начнем с самого простого его вида. Еще раз рассмотрим график движения муравья, приведенный на рис. 11. Мы видим, что характер движения муравья менялся дважды. Сначала он двигался, пробегая 1 см за каждую секунду, затем стоял на месте, потом снова двигался в положительном направлении оси X, но уже быстрее, чем раньше, - пробегая за каждую секунду 2 см. В целом, за семь секунд движения муравья было неравномерным: муравей то бежал, то останавливался.

Вместе с тем в первые три секунды он пробегал по 1 см за каждую секунду. Значит, в первые три секунды за равные промежутки времени (по одной секунде) муравей пробегал в одном и том же направлении равные расстояния (по одному сантиметру). Если это условие будет выполняться для любых равных промежутков времени (например, каждые полсекунды, четверть секунды и т. д.), то движение муравья будет равномерным.

Прямолинейное движение тела называют равномерным, если тело за любые равные промежутки времени проходит равные расстояния в одном и том же направлении.

В соответствии с этим определением движение муравья в последние две секунды также являлось равномерным: он за любые равные промежутки времени пробегал равные расстояния в одном направлении.

Отметим, что в данном определении, как и в любом другом, каждое слово имеет важное значение. Так, например, если убрать слова «в одном и том же направлении», то движение тела может оказаться неравномерным, даже если это тело будет проходить равные расстояния за любые равные промежутки времени. Это произойдет в случае, если тело в некоторый момент времени изменит направление своего движения на противоположное.

Чтобы лучше понять данное определение, рассмотрим конкретный пример равномерно движущегося тела.

Пусть по прямолинейной дороге, как показано на рис. 13, катится мальчик на велосипеде. Будем следить за движением фары этого велосипеда, считая ее точечным телом.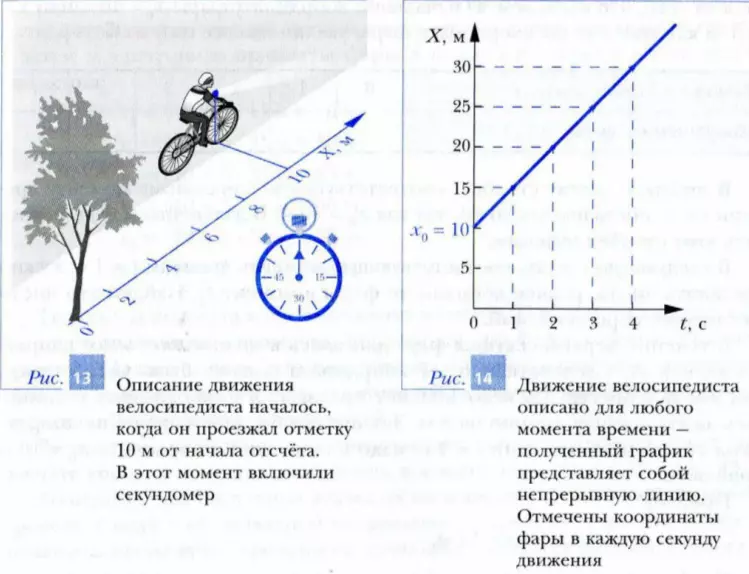

Как мы уже знаем, для описания механического движения тела (фары) необходимо ввести систему отсчета. Выберем в качестве тела отсчета землю, по которой движется велосипед. За начало отсчета примем место, где растет дерево на обочине дороги. Координатную ось направим от выбранного начала отсчета параллельно дороге по направлению движения велосипеда. В качестве единицы длины выберем 1 м. Включим секундомер в тот момент, когда фара была в 10 м от начала отсчета, и будем фиксировать ее координату в последующие моменты времени. Пусть в результате проведенных измерений мы получили график изменения координаты фары с течением времени, изображенный на рис. 14.

Видно, что линия, описывающая зависимость координаты фары от времени, является прямой. Для того чтобы описать движение фары, прежде всего отметим, что она двигалась в положительном направлении оси X. Кроме того, за каждую (любую) секунду движения ее координата увеличивалась на 5 м (т. е. на одинаковую величину), за каждые две секунды — на 10 м и т. д. Следовательно, в соответствии с данным в начале этого параграфа определением мы имеем дело с прямолинейным равномерным движением.

Теперь вспомним еще об одном способе описания движения — табличном. Сделаем заготовку для таблицы и заполним ее. При этом значения координаты тела в разные моменты времени мы будем находить не из графика, а из того, что мы знаем: а) начальную координату фары x₀ = 10 м и б) то, что за каждую секунду координата фары увеличивалась на 5 м.

Для удобства и краткости записи часто используют переменные с индексом. Например, ранее при описании движения муравья мы использовали для обозначения его координаты символ x_м (читается «икс эм» или «икс с индексом эм»). При описании движения велосипедиста для обозначения координаты фары в начальный момент времени (t = 0) будем использовать символ x0 (читается «икс нулевое» или «икс с индексом ноль»). Соответственно для координаты фары в момент времени t₁ — символ x₁ (читается «икс один»).

В нижнюю клетку столбца, соответствующую начальному моменту времени t = 0, поставим число 10, так как x₀ = 10 м. В дальнейшем будем называть этот столбец нулевым.

В следующую клетку, соответствующую моменту времени t = 1 с, нужно поставить число, равное координате фары в момент t₁. Найдем это число из следующих рассуждений.

В течение первой секунды фара двигалась в положительном направлении оси X. Следовательно, ее координата должна была увеличиться. Так как за одну секунду велосипедист проезжал 5 м, координата увеличилась за эту секунду именно на 5 м. Значит, чтобы найти значение координаты x1 в момент времени t = 1 с, надо к начальной координате x₀ = 10 м прибавить 5 м.

Поэтому

x₁ = (10 + 5) м = 15 м.

Чтобы найти координату x₂ в момент t = 2 с, вычислим, на сколько изменилась ее координата за две секунды после включения секундомера. Поскольку за каждую секунду фара смещается на 5 м, то за две секунды она переместится на (5 * 2) м = 10 м. Так как фара движется в положительном направлении оси X, то ее координата за две секунды увеличится на (5 * 2) м.

Разность между конечным и начальным значениями координаты называют изменением координаты. В данном случае изменение координаты фары за две секунды движения (от момента t₀ до момента t₂) составило x₂ – x₀ = 10 м.

Таким образом,

x₂ = (10 + 5 * 2) м = 20 м.

Проводя аналогичные рассуждения, можно найти изменения координаты фары за три, четыре, пять и шесть секунд движения велосипедиста, а затем и значения координаты фары в каждую из первых шести секунд движения:

x₁ = (10 + 5 * 2) м = 15 м,
x₂ = (10 + 5 * 2) м = 20 м,
x₃ = (10 + 5 * 3) м = 25 м,
x₄ = (10 + 5 * 4) м = 30 м,
x₅ = (10 + 5 * 5) м = 35 м,
x₆ = (10 + 5 * 6) м = 40 м.

Теперь мы подошли к очень важному моменту. Посмотрим внимательно на полученные нами выражения для координаты фары в разные моменты времени. Можно сказать, что они похожи и написаны по одному правилу. Или, как говорят физики, в этом случае наблюдается определенная закономерность. В чем же она заключается?

Рассмотрим подробно, что представляет собой каждое из чисел при расчете координаты фары, например, в момент времени t = 7 c (рис. 15).

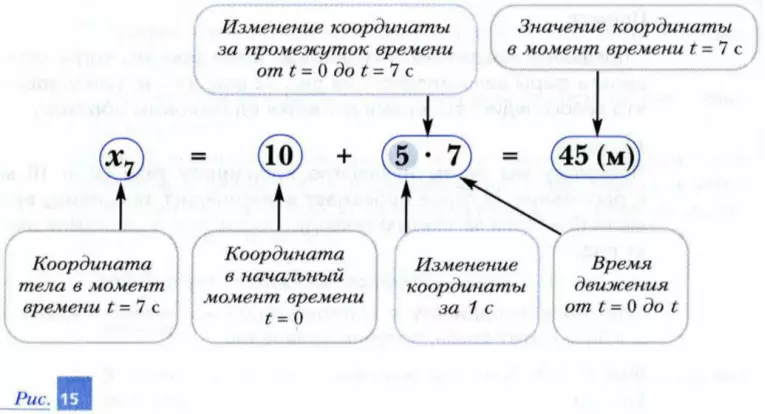
Во-первых, для получения значения координаты фары в любой момент времени t надо к ее начальной координате x₀ прибавить изменение координаты за промежуток времени от начального момента времени t = 0 до t.

Во-вторых, при равномерном прямолинейном движении это изменение координаты можно получить, если умножить изменение координаты за одну секунду (в нашем случае — это 5 м) на число секунд, прошедших от момента t = 0 до момента t (в нашем случае — это 7 с).

Таким образом, мы получаем выражение, которое позволяет рассчитать координату x фары в любой момент времени t:

x = 10 + 5 * t.

Следовательно, если мы знаем начальную координату и изменение его координаты за каждую секунду, мы можем получить зависимость координаты тела от времени t.

Выражение, описывающее зависимость координаты тела от времени, называют законом движения этого тела. Если в это выражение подставить конкретное значение времени t, то оно превратится в уравнение, позволяющее вычислить координату тела в этот момент.

Отметим, что если мы знаем закон движения тела, то мы можем решить и обратную задачу — определить момент времени, в который тело будет находиться в точке с заданной координатой.

Пример
Определить показание секундомера в тот момент, когда координата фары велосипедиста на рис. 13 равна 60 м, при условии, что велосипедист все время движется одинаковым образом.
Решение
Поскольку мы знаем начальную координату тела (x₀ = 10 м) и расстояние, которое проезжает велосипедист за единицу времени (5 метров за каждую секунду), то закон его движения имеет вид:
x = 10 + 5 * t, где t — искомое показание секундомера.
Подставив координату в интересующий нас момент времени x = 60 м в этот закон, получим уравнение:
60 = 10 + 5 * t,
60 – 10 = 5 * t,
50 = 5 * t,
t = 10 с.
Ответ: на секундомере будет 10 с.

В полученном нами выражении x = 10 + 5 * t изменение координаты за единицу времени является постоянной величиной, так как мы рассматриваем прямолинейное равномерное движение. Эту величину принято обозначать латинской буквой v. Поэтому найденную нами зависимость в аналитической форме (в виде формулы) можно записать в виде:

x = x₀ + v * t.

Представление зависимости координаты тела от времени в виде формулы — еще одни,третий способ описания движения. Его называют аналитическим.

Итоги

Прямолинейное движение тела называют равномерным, если тело за любые равные промежутки времени проходит равные расстояния в одном и том же направлении.

Изменение координаты тела за промежуток времени от момента t₁ до момента t₂ называют разность x₂ – x₁ между конечным и начальным значениями координаты.

Прямолинейное равномерное движение характеризуется тем, что изменение координаты тела за единицу времени (ее обычно обозначают латинской буквой v) есть величина постоянная.

График зависимости координаты x тела от времени t для такого движения представляет собой прямую линию.

При этом зависимость координаты тела от времени имеет вид:

x = x₀ + v * t,

где x₀ — начальная координата тела, t — момент времени после начала движения, v — постоянная величина, равная изменению координаты тела за единицу времени, x — координата тела в момент времени t.