Путь при прямолинейном равноускоренном движении в одном направлении
Изучение прямолинейного равноускоренного движения мы начнем со случая, когда тело движется все время в положительном направлении оси X. Нам известно, что при этом путь s, модуль перемещения тела |Δx| и изменение его координаты Δx = xк - x0 равны между собой. Итак, пусть тело (например, автомобиль) движется прямолинейно с постоянным ускорением a в положительном направлении оси X так, как показано на рис. 57. В начальный момент t = 0 автомобиль имел значение скорости v0. Тогда значение его скорости v в любой последующий момент времени t равно
v = v0 + a · t.
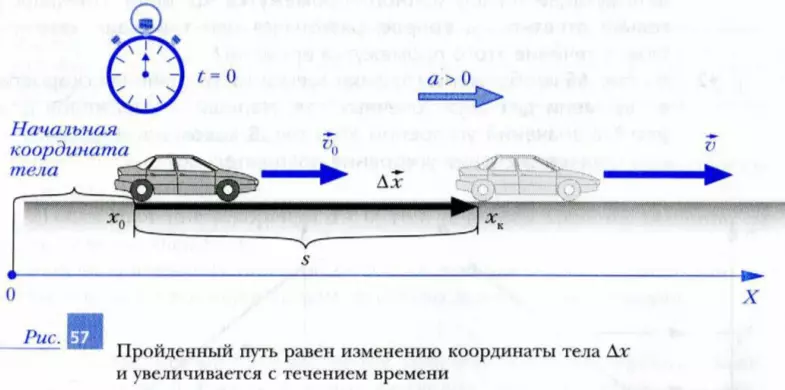
График этой зависимости значения скорости от времени показан на рис. 58.
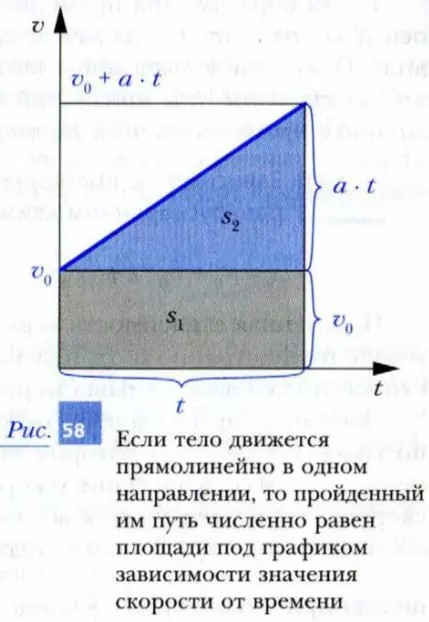
Как вы помните, при прямолинейном равномерном движении в одном направлении пройденный телом путь s численно равен площади под графиком зависимости значения скорости от времени. Можно показать, что это верно для любого прямолинейного движения в одном направлении. Поэтому путь, пройденный движущимся равноускоренно телом за время t, начиная с момента t = 0, численно равен площади фигуры под графиком (см. рис. 58). Эта фигура состоит из серого прямоугольника и синего прямоугольного треугольника. Площадь прямоугольника, как известно, равна произведению его сторон: s1 = v0 · t. А площадь прямоугольного треугольника равна половине площади прямоугольника со сторонами (a · t) и t. Следовательно, эта площадь равна
s2 = ((a · t) · t) / 2.
Таким образом, площадь фигуры под графиком равна сумме площадей этих фигур: s = s1 + s2. Поэтому пройденный телом за время t путь равен
s = s1 + s2 = v0 · t + (a · t2) / 2.
Если тело все время прямолинейно равноускоренно движется в положительном направлении оси X, имея значения начальной скорости v0 и ускорения a, то пройденный телом за время t путь равен
s = v0 · t + (a · t2) / 2.
При этом пройденный телом путь s численно равен площади под графиком зависимости значения скорости от времени.
Воспользуемся полученным нами результатом для ответа на основной вопрос кинематики – определения координаты движущегося тела в произвольный момент времени. Как мы уже отмечали в начале параграфа, если тело все время движется в положительном направлении оси X, то пройденный им путь s равен модулю совершенного им перемещения |Δx| и изменению его координаты Δx. Поэтому можно утверждать, что s = x - x0 или
x - x0 = v0 · t + (a · t2) / 2.
Перенося (-x0) в правую часть с противоположным знаком, получим:
x = x0 + v0 · t + (a · t2) / 2.
Таким образом, при прямолинейном равноускоренном движении вдоль оси X координата x тела меняется с течением времени по указанному правилу. Полученное выражение называют зависимостью координаты тела от времени при прямолинейном равноускоренном движении (или законом прямолинейного равноускоренного движения).
Зависимость координаты тела от времени при прямолинейном равноускоренном движении имеет вид:
x = x0 + v0 · t + (a · t2) / 2.
Полученная зависимость верна и для движения, при котором значение ускорения постоянно и отрицательно (a
Например, пусть значение скорости тела изменяется с течением времени по закону v = 5 - 7 · t, в котором значение скорости в начальный момент времени v0 = 5 м/с, а значение ускорения a = -7 м/с2. В этом случае значение скорости тела уменьшается во времени. Тогда, если, например, начальная координата тела x0 = 3 м, то координата x этого тела изменяется со временем по закону x = 3 + 5 · t - (7 · t2) / 2, где x измеряют в метрах, а t — в секундах.
Итоги
Если тело все время прямолинейно равноускоренно движется в положительном направлении оси X, имея значения начальной скорости v0 и ускорения a, то пройденный телом за время t путь равен
s = v0 · t + (a · t2) / 2.
Если при этом начальная координата тела равна x0, то его координата x в момент времени t может быть найдена по формуле:
x = x0 + v0 · t + (a · t2) / 2,
а значение скорости в тот же момент времени – по формуле:
v = v0 + a · t.
Вопросы
- По какой формуле рассчитывают путь, пройденный телом за данный промежуток времени при прямолинейном равноускоренном движении в положительном направлении оси X?
- Расскажите, как, имея график зависимости значения скорости прямолинейного равноускоренного движения от времени, найти пройденный телом путь.
Упражнения
- Найдите координаты прямолинейно равноускоренно движущегося тела в моменты времени 3, 5 и 10 с, если известно, что его начальная координата x0 = 4 м, значение начальной скорости v0 = 3 м/с, а значение ускорения a = 2 м/с2. Найдите путь, пройденный телом за 3; 5; 10 с.
- Постройте график зависимости от времени значения скорости тела, движение которого описано в упражнении 1. Найдите, используя график, путь, пройденный телом за 3; 5; 10 с.
- Напишите выражение для зависимости координаты x тела от времени при равноускоренном движении, если в начальный момент времени t = 0 была равна нулю: а) его координата; б) его скорость.
- Нарисуйте, как будут выглядеть графики зависимости от времени значения скорости тела, движение которого задано в упражнении 3.
- Проведите анализ зависимости координаты тела от времени при прямолинейном равноускоренном движении, ответив на вопросы. Как будут изменяться значения x, если поочередно увеличить: а) начальную координату x0; б) значение начальной скорости v0; в) значение ускорения a; г) время t? Если поочередно уменьшить соответствующие величины?
