Решение задач кинематики в общем виде

Мы с вами научились решать задачи с конкретными числовыми значениями. Освоим решение задач, в которых величины, характеризующие движение тел (начальные координаты, скорости и т. п.), определены не численно, а заданы в буквенном виде. В этом случае говорят о решении задачи в общем виде.

Решение задач в общем виде очень распространено. Оно позволяет упростить преобразования выражений, которые могут быть довольно громоздкими, избегать промежуточных вычислений, выявить взаимосвязь между физическими величинами.

Рассмотрим такое решение на примере задачи «встреча».

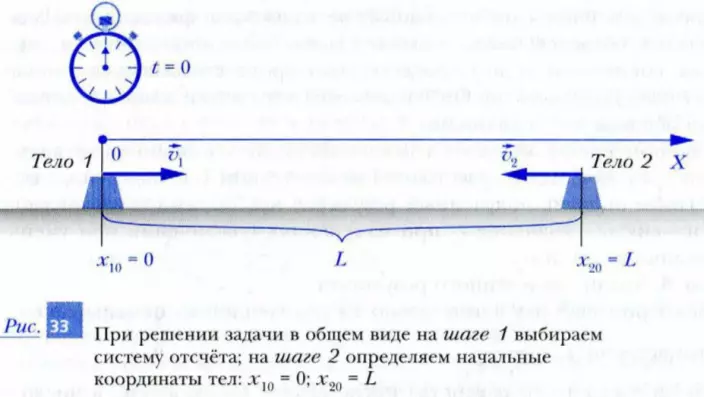
Пусть два точечных тела 1 и 2 движутся навстречу друг другу относительно земли со скоростями v₁ и v₂ соответственно (рис. 33). В момент начала наблюдения расстояние между телами равно L. Необходимо определить, через какое время после начала наблюдения (когда?) произойдет встреча этих тел.

Используем известный нам метод решения задач кинематики.

Шаг 1. Выбор системы отсчета. В качестве начала отсчета выберем то место на дороге, где находилось в начальный момент первое тело. Координатную ось X направим от этого места вдоль дороги в направлении второго тела. Отметим, что единицы длины должны быть те же, в которых задано расстояние L между телами. Часы включим в момент начала наблюдения.

Шаг 2. Определим начальные координаты тел. Ясно, что в выбранной нами системе отсчета x₁₀ = 0, а x₂₀ = L.

Шаг 3. В соответствии с условием задачи в выбранной системе отсчета значение скорости тела 1 положительно и равно v₁. Значение скорости тела 2 отрицательно и равно -v₂, так как это тело движется в отрицательном направлении оси X. Здесь v₁ и v₂ – модули соответствующих скоростей.

Шаг 4. Запишем зависимости координат равномерно движущихся тел 1 и 2 от времени:

x₁ = x₁₀ + v₁ · t = 0 + v₁ · t,
x₂ = x₂₀ - v₂ · t = L - v₂ · t.

Шаг 5. Представим в виде уравнения условие задачи – равенство координат двух тел в момент встречи:

x₁ = x₂.

Шаг 6. Запишем вместе полученные уравнения, присвоив каждому из них номер и название:

x₁ = v₂ · t, (1) (закон движения тела 1)
x₂ = L - v₂ · t, (2) (закон движения тела 2)
x₁ = x₂. (3) (условие встречи тел 1 и 2)

Шаг 7. Решение уравнений.

Для решения полученных уравнений подставим в условие встречи – уравнение (3) – выражения для x₁ и x₂:

v₁ · t = L - v₂ · t.

Решим полученное уравнение:

v₁ · t + v₂ · t = L,
(v₁ + v₂) · t = L,
t = t_в = L / (v₁ + v₂).

Итак, мы получили значение момента времени встречи двух тел.

Теперь перейдем к очень важному не только для физики, но и для самых разных областей человеческого знания (экономики, бизнеса, планирования, социологии и др.) процессу. Этот процесс называется анализом полученного результата. Он заключается в изучении зависимости между интересующими нас величинами.

В данном случае мы имеем зависимость значения момента времени встречи t_в от начального расстояния между телами L и модулей их скоростей. Чтобы оценить полученный результат, необходимо исследовать, как будет изменяться значение t_в при изменениях (увеличении или уменьшении) величин L, v₁ и v₂.

Шаг 8. Анализ полученного результата.

Посмотрим еще раз внимательно на полученное нами выражение для момента встречи: t_в = L / (v₁ + v₂).

Правая часть этого равенства представляет собой дробь, в числителе которой стоит начальное расстояние между сближающимися телами L, а в знаменателе – сумма модулей скоростей тел 1 и 2. Для начала зададим себе вопрос: как изменится время tв через которое произойдет встреча, если в условии задачи увеличить L, например, в 10 раз, а модули скоростей v₁ и v₂ оставить неизменными?

Ясно, что в этом случае в 10 раз увеличится числитель дроби в выражении для t_в, а ее знаменатель останется неизменным. Следовательно, значение дроби увеличится в 10 раз, т. е. увеличится в 10 раз время tв, через которое произойдет встреча.

Напротив, если L уменьшить, например, в 2 раза, оставив модули скоростей v₁ и v₂ неизменными, то числитель дроби уменьшится в 2 раза при неизменном знаменателе. Следовательно, встреча произойдет через время, в два раза меньшее.

Вывод 1. Чем больше начальное расстояние между телами, тем позже произойдет их встреча, и наоборот, чем меньше это расстояние, тем раньше данные тела встретятся.

В частности, если задать начальное расстояние между телами равным нулю, то, подставив это значение в выражение для t_в, мы получим t_в = 0 / (v₁ + v₂) = 0. То есть встреча произойдет в момент начала наблюдения.

Проанализируем, как изменится время встречи tв, если изменить модули скоростей тел v₁ и v₂, оставив неизменным начальное расстояние L. Допустим, модули скоростей движущихся навстречу друг другу тел увеличатся в 2 раза. Тогда их сумма v₁ + v₂, стоящая в знаменателе, также увеличится вдвое. В этом случае вся дробь при неизменном числителе L уменьшится в 2 раза. Следовательно, встреча двух тел произойдет через вдвое меньшее время. Наоборот, если модули скоростей обоих тел уменьшить, например, в 10 раз при неизменном L, то встреча состоится через время t_в, в 10 раз большее первоначального.

Вывод 2. Чем больше модули скоростей v₁ и v₂ движущихся навстречу друг другу тел, тем раньше тела встретятся, и наоборот, чем меньше модули их скоростей, тем позже произойдет встреча. Например, если взять предельный случай, когда v₁ = v₂ = 0, то для времени встречи получится следующее выражение:

t_в = L / (v₁ + v₂) = L / (0 + 0) = L/0.

Мы получили деление на нуль. Это означает, что встречи не будет. Понятно: если скорости тел равны 0, то они покоятся.

Отметим, что время встречи зависит от суммы модулей скоростей тел (v₁ + v₂). Эту сумму можно назвать модулем скорости сближения движущихся навстречу друг другу тел. Как вы понимаете, модуль скорости сближения численно равен уменьшению расстояния между телами за единицу времени.

В заключение проанализируем еще одну ситуацию. Допустим, начальное расстояние между телами увеличилось в два раза. Одновременно увеличились вдвое модули скоростей сближающихся тел, т. е. в два раза увеличилась скорость сближения. Как вы понимаете, в этом случае в два раза увеличатся и числитель, и знаменатель выражения для расчета времени встречи. Известно, что при умножении числителя и знаменателя дроби на одно и то же число значение этой дроби не изменяется. Следовательно, в этом случае момент встречи останется неизменным.

Если вы вдумаетесь в полученные выводы 1 и 2, то поймете, что они соответствуют здравому смыслу и нашему жизненному опыту. В этом случае физики говорят, что в задаче получен ответ, который имеет физический смысл.

Итоги

При решении задач кинематики в общем виде нужно придерживаться следующего алгоритма:

1) выбрать систему отсчета; 2-3) определить начальные координаты и значения скоростей движения тел в этой системе отсчета; 4) записать зависимости координат тел от времени; 5) записать в виде уравнения условие задачи; 6) объединить уравнения; 7) решить эти уравнения; 8) провести анализ полученного результата (после чего выяснить, имеет ли полученный результат физический смысл); 9) если в условии задачи даны числовые значения, необходимо подставить их в полученное выражение и получить числовой ответ.

Анализ полученного результата заключается в исследовании зависимости искомой величины от входящих в ответ величин.

Конечной целью проведения анализа является ответ на вопрос: имеет ли физический смысл полученное при решении задачи выражение?

Упражнения

1. Найдите в общем виде время окончания погони полицейского за грабителем t_п (задача «погоня»). Используйте данные, приведенные на рис. 34.

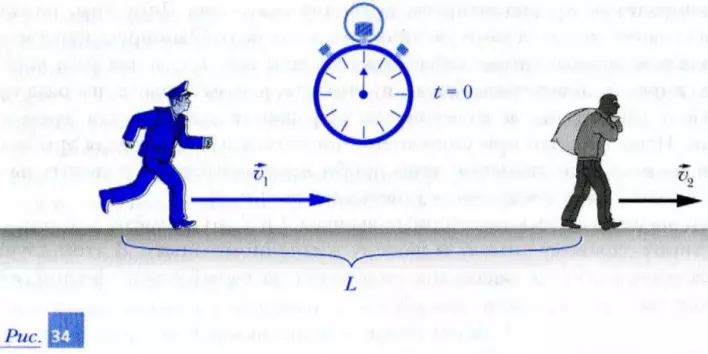
2. Используя данные из упражнения 1, проведите анализ выражения для времени погони t_п = L / (v₁ - v₂), ответив на вопросы:
а) как зависит время окончания погони tп от начального расстояния между полицейским и грабителем?
б) увеличится или уменьшится время окончания погони t_п, если увеличится: скорость полицейского v₁; скорость грабителя v₂?
в) догонит ли полицейский грабителя, если: v₁ > v₂; v₁ < v₂; v₁ = v₂?
г) имеет ли физический смысл полученное нами выражение для t_п?
д) определите скорость сближения полицейского и грабителя.

3. Найдите в общем виде выражение для времени обгона, рассмотрев ситуацию из предыдущего параграфа.

4. Используя данные из упражнения 3, проведите анализ выражения t_об = (l₁ + l₂) / (v₂ - v₁) и ответьте на следующие вопросы:
а) увеличится или уменьшится время обгона t_об, если увеличится длина: обгоняемого тела l₁; обгоняющего тела l₂?
Сделайте выводы. Какой автобус легче обогнать: короткий или длинный? На каком автомобиле быстрее завершается обгон: на коротком или на длинном?
б) увеличивается или уменьшается время обгона при увеличении: скорости обгоняемого v₁; скорости обгоняющего v₂?
Сделайте выводы. Какой автомобиль можно быстрее обогнать: едущий быстро или медленно? На каком автомобиле быстрее завершается обгон: на едущем быстро или медленно?