Движение тел относительно друг друга. Задача «погоня»

Рассмотрим теперь, как будет выглядеть решение задачи «погоня» при использовании системы отсчета, связанной с одним из движущихся тел.

Диспетчер, взглянув на монитор, увидел, что за паровозом, движущимся со скоростью |v_п| = 60 км/ч, следует электровоз со скоростью |v_э| = 90 км/ч. Через какое время t_д электровоз догонит паровоз, если расстояние между ними в начальный момент l = 120 км?

Шаг 1. Введем систему отсчета следующим образом. В качестве тела отсчета выберем электровоз. Координатную ось X направим от электровоза вдоль железнодорожного полотна в направлении к паровозу. За единицу длины примем 1 км. Часы включим в момент, когда диспетчер взглянул на монитор и увидел картину, изображенную на рис. 41.

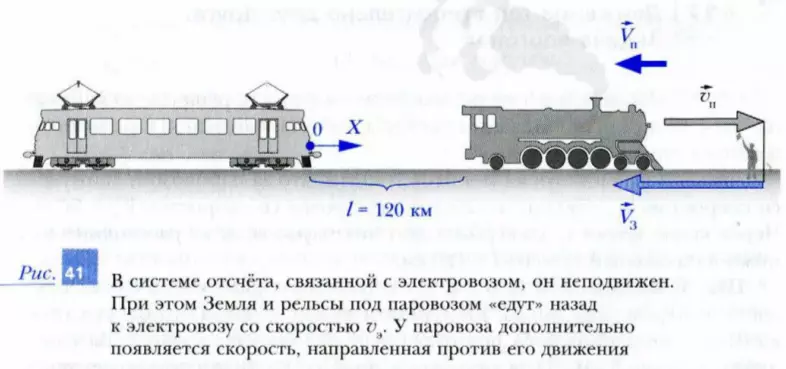
Шаг 2. В выбранной системе отсчета электровоз неподвижен, и его координата в начальный момент и все последующие моменты времени равна x_э0 = x_э = 0. Начальная координата паровоза в выбранной системе отсчета x_п0 = l = 120 км.

Шаг 3. Определим значение скорости движении паровоза в выбранной системе отсчета, учитывая, что в ней:
1) Земля движется навстречу электровозу, т. е. в отрицательном направлении координатной оси X;
2) модуль скорости этого движения равен данному в задаче модулю скорости движения электровоза относительно Земли |v_э| = 90 км/ч.

Следовательно, значение скорости Земли в выбранной системе отсчета V_з = -90 км/ч. Модуль скорости паровоза относительно Земли по условию задачи |v_п| = 60 км/ч. Отметим, что эта скорость направлена в положительном направлении оси X, т. е. за каждый час паровоз проезжает по Земле 60 км в положительном направлении оси X.

При атом за тот же час Земля, по которой едет паровоз, проходит 90 км в противоположном (т. е. отрицательном) направлении оси X. Следовательно, за каждый час координата паровоза изменяется на (60 - 90) км = -30 км. Иначе говоря, паровоз за каждый час приближается к электровозу на 30 км.

Таким образом, в нашей системе отсчета паровоз движется в отрицательном направлении оси X со скоростью, имеющей значение V_п = -30 км/ч.

С точки зрения сложения значений скоростей это выглядит следующим образом (см. рис. 41). К положительному значению скорости паровоза относительно Земли v_п = 60 км/ч прибавляется отрицательное значение скорости Земли в выбранной системе отсчета V_з = -90 км/ч. В результате значение скорости паровоза в системе отсчета, связанной с электровозом:

V_п = 60 + (-90) = -30 (км/ч).

Шаг 4. Запишем законы движения паровоза и электровоза:

x_п = x_п0 + V_п · t = 120 - 30 · t,
x_э = x_э0 = 0.

Шаг 5. Напишем уравнение, выражающее условие окончания погони:

x_п = x_э.

Шаг 6. Объединим полученные уравнения, присвоив каждому номер и название:

x_п = 120 - 30 · t, (1) (закон движения паровоза)
x_э = 0, (2) (закон движения электровоза)
x_п = x_э. (3) (условие окончания погони)

Шаг 7. Решим полученные уравнения, подставив в условие окончания погони – уравнение (3) – координаты x_п и x_э из уравнений (1) и (2):

120 - 30 · t = 0,
t_д = t = 120/30 = 4 (ч).

Таким образом, электровоз догонит паровоз через 4 часа после того, как диспетчер взглянул на монитор.

Итоги

При выборе начала отсчета, связанного с одним из движущихся тел, решение задач «встреча» и «погоня» резко упрощается, так как фактически эти задачи сводятся к задаче о движении одного тела.

Упражнения

1. Объясните приведенное на рис. 42 графическое решение задачи «погоня» электровоза за паровозом. Ответьте на вопросы:

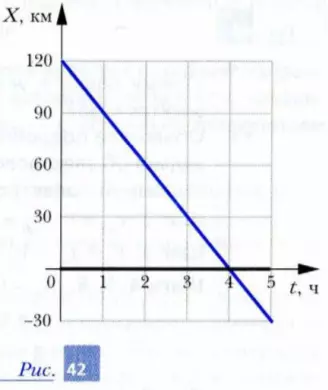
а) каким цветом на графике изображены законы движения: электровоза; паровоза?
б) чему равна начальная координата в системе отсчета, связанной с электровозом: у электровоза; у паровоза?
в) чему равно значение скорости в системе отсчета, связанной с электровозом: электровоза; паровоза?
г) где на графике находится точка окончания погони? В какой момент времени после начала погони происходит встреча?
д) какой знак будет иметь координата паровоза в момент времени t = 5 ч после начала погони, если движение тел будет продолжаться? Чему она будет равна?

2. Используя рис. 43, решите задачу о погоне электровоза за паровозом, рассмотренную в этом параграфе, выбрав систему отсчета, начало которой совпадает с паровозом, а координатная ось X совпадает с направлением скорости паровоза относительно Земли.

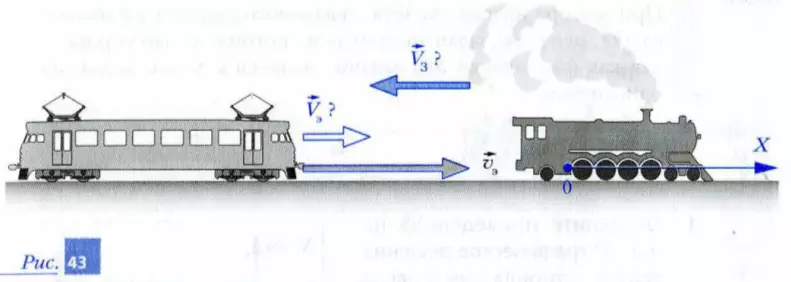
Прежде чем начать решать задачу, ответьте на вопросы:
а) положительна или отрицательна начальная координата электровоза? Чему она равна?
б) с какой скоростью (в каком направлении) движется Земля в указанной системе отсчета?
в) чему равно в указанной системе отсчета значение скорости электровоза?

3. Объясните подробно приведенное ниже в общем виде решение задачи об электровозе, догоняющем паровоз, в системе отсчета, связанной с электровозом, начиная со второго шага.

Шаг 2. x_э0 = 0, x_п0 = l.
Шаг 3. V_п = v_п + V_з = v_п - v_э.
Шаги 4, 5, 6. x_п = l + (v_п - v_э) · t, (1)
x_э = 0, (2)
x_п = x_э. (3)
Шаг 7. l + (v_п - v_э) · t = 0, t_д = t = l / (v_э - v_п).

4. Проведите анализ полученного в предыдущей задаче результата, т, е. выполните шаг 8. Ответьте на вопрос чему равно значение скорости сближения электровоза и паровоза?