Решение задач кинематики. Задача «обгон»

Рассмотрим еще одну очень важную с практической точки зрения задачу. Пусть по прямой двухполосной дороге едут грузовик с прицепом и легковой автомобиль. Модули их скоростей равны соответственно |v_г| = 20 м/с и |v_л| = 30 м/с. Известно, что длина легкового автомобиля l₁ = 5 м, а грузовик вместе с прицепом имеет длину l₂ = 35 м. При этом легковой автомобиль, значение скорости которого больше, совершает обгон грузовика. Эта ситуация изображена на рис. 31.

Из сказанного ясно, что в задаче «обгон» принципиальную роль играют размеры тел. Поэтому для описания движения грузовика и легковушки нам надо выбрать конкретные точки этих тел. Кроме того, необходимо установить, какие моменты времени являются началом и окончанием обгона.

Моментом начала обгона (положение I) мы будем называть тот момент времени, когда самая передняя точка A («нос») легкового автомобиля поравнялась с самой задней точкой B («хвостом») прицепа грузовика. Моментом окончания обгона назовем тот момент времени, когда точка C (« хвост» ) легкового автомобиля поравняется с точкой D («носом») грузовика. Этот момент соответствует положению II на рис. 31.

Спрашивается:
1. В течение какого промежутка времени будет происходить обгон?
2. Какие расстояния проедут за время обгона легковой автомобиль и грузовик?

Чтобы ответить на поставленные вопросы, воспользуемся аналитическим методом решения кинематических задач.

Шаг 1. Введем систему отсчета (рис. 32). В качестве начала отсчета выберем камень, лежащий на обочине дороги напротив того места, где поравнялись точки A и B в момент начала обгона. Координатную ось X направим от этого камня параллельно дороге в сторону движения машин. В качестве единицы длины выберем 1 м. Часы (секундомер) включим в момент начала обгона.

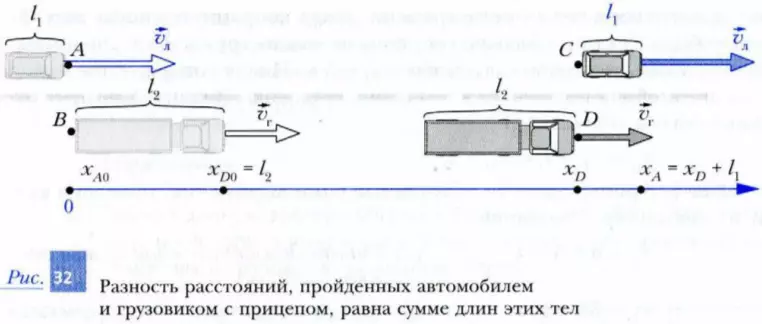
По условию задачи грузовик и легковой автомобиль имеют конкретные размеры. Поэтому мы не можем считать наши тела точечными. Значит, для описания движения этих тел надо на каждом из них выбрать конкретные точки и далее следить за движением этих точек. В качестве точки, характеризующей положение легкового автомобиля, выберем точку A (его «нос»). Для описания положения грузовика с прицепом выберем точку D (соответственно «нос» грузовика). Теперь, если мы будем говорить, что координата легкового автомобиля равна, например, нулю, то это значит, что равна нулю координата его «носа» – точки A. А если мы скажем, что координата грузовика равна, например, сорока метрам, значит, говорится о координате «носа» грузовика – точке D. То есть мы будем следить за движением «носов» обоих движущихся тел.

Шаг 2. Определим начальные координаты точек A и D, которые характеризуют положение соответственно легкового автомобиля и грузовика с прицепом. Из рис. 32 видно, что x_A0 = 0, а x_D0 = l₂ = 35 м. Таким образом, в момент начала обгона «нос» грузовика опережает «нос» легкового автомобиля ровно на длину грузовика с прицепом l₂ = 35 м.

Шаг 3. В условии задачи даны модули скоростей легкового автомобиля и грузовика относительно дороги. При этом в выбранной системе отсчета координаты обоих тел увеличиваются. Следовательно, значения их скоростей положительны и равны соответственно v_л = 30 м/с и v_г = 20 м/с.

Шаг 4. Напишем зависимости координат, точек A и D, от времени в выбранной системе отсчета:

x_A = x_A0 + v_л · t = 0 + 30 · t,
x_D = x_D0 + v_г · t = l₂ + v_г · t = 35 + 20 · t.

Шаг 5. Представим в виде уравнения условие окончания обгона. Если мы внимательно посмотрим на рис. 32 (положение II), то поймем, что обгон закончится в тот момент времени, когда координата «носа» легкового автомобиля xA станет больше координаты «носа» грузовика x_D ровно на величину длины легкового автомобиля l₁ = 5 м. Иначе говоря, «хвост» легкового автомобиля поравняется с «носом» грузовика. Значит, в момент окончания обгона (при t = t_об)

x_A = x_D + l₁ = x_D + 5.

Шаг 6. Запишем вместе полученные нами выражения, присвоив каждому из них номер и название:

x_A = 0 + 30 · t, (1) (закон движения «носа» легкового автомобиля)
x_D = 35 + 20 · t, (2) (закон движения «носа» грузовика)
x_A = x_D + 5. (3) (условие окончания обгона)

Шаг 7. Решение уравнений.

Для нахождения момента времени, соответствующего окончанию обгона, подставим в уравнение (3) выражения для x_A и x_D из уравнений (1) и (2):

0 + 30 · t = 35 + 20 · t + 5,
30 · t - 20 · t = 35 + 5,
t = (35 + 5) / (30 - 20) = 4 (с).

Таким образом, через время t_об = 4 с после включения секундомера обгон будет завершен.

Найдем, какое расстояние прошел за это время «нос» легкового автомобиля (точка A). Для этого определим его координату в момент времени t = 4 с. Подставив данное значение времени в закон движения точки A, получим:

x_A = 0 + 30 · t = 0 + 30 · 4 = 120 (м).

Так как начальная координата точки A x_A0 = 0, «нос» автомобиля за время обгона прошел расстояние l_A = 120 м.

Теперь определим, какое расстояние за время совершения обгона легковым автомобилем прошел грузовик. Для этого найдем координату его «носа» (точки D) в момент окончания обгона. Подставив значение времени окончания обгона t = 4 с в закон движения точки D, получим:

x_D = 35 + 20 · 4= 115 (м).

Так как начальная координата «носа» грузовика равнялась x_D0 = 35 м, то грузовик за время обгона прошел расстояние

l_D = x_D - x_D0 = 115 - 35 = 80 (м).

Таким образом, разность пройденных «носом» легкового автомобиля (точкой A) и «носом» грузовика (точкой D) расстояний l_A - l_D = 120 - 80 = 40 (м), что составляет сумму длин обгоняемого и обгоняющего тел:

l₁ + l₂ = 5 + 35 = 40 (м).

Упражнения
1. Решите данную задачу «обгон» табличным способом. Для этого, используя записанные в шаге 4 законы движения легкового автомобиля и грузовика, заполните таблицу.

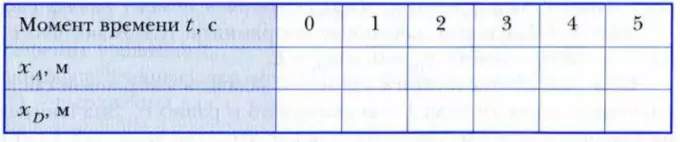
2. Используя данные, полученные в предыдущем упражнении, или законы движения тел (шаг 4), постройте графики зависимости от времени координат точек A и D, характеризующих положения легкового автомобиля и грузовика. Укажите на графике точку (время и координату), в которой завершился процесс обгона.

3. Определите, в течение какого времени автобус длиной l_a = 20 м, движущийся с постоянной скоростью |v_a| = 35 м/с, будет обгонять грузовик длиной l_г = 25 м, если скорость грузовика не изменяется и равна |v_г| = 30 м/с. Задачу решите: а) аналитическим; б) табличным; в) графическим способами.

4. Зависит ли время обгона грузовика легковым автомобилем от размеров (длины) этих транспортных средств? Если зависит, то как?