Ускорение

Мы выяснили, что движущийся по дороге автомобиль практически все время изменяет свою скорость. Так, если во время движения водитель нажимает на педаль тормоза, скорость автомобиля уменьшается. Если водитель нажимает на педаль газа, скорость автомобиля, наоборот, возрастает. При этом под словом «скорость» мы подразумеваем, как это было отмечено в предыдущем параграфе, мгновенную скорость.

Таким образом, если водитель нажмет на педаль тормоза сильно, скорость автомобиля начнет изменяться быстро, и вскоре он остановится. При слабом нажатии на тормоз скорость автомобиля будет уменьшаться медленно, и до момента остановки, когда скорость автомобиля станет равной нулю, пройдет больше времени (рис. 52). Можно сказать, что изменение скорости при этом происходит с разной быстротой.

Из приведенного примера ясно, что быстрота изменения скорости определяется начальным и конечным значениями скорости и промежутком времени, за который произошло изменение скорости.

Величину, характеризующую быстроту изменения скорости, называют ускорением.

При решении задач о прямолинейном движении тел используют понятие «значение ускорения».

Значением среднего ускорения тела за промежуток времени tк - t0 называют отношение изменения значения скорости тела за данный промежуток времени к длительности этого промежутка.

a_ср = (v_к - v₀) / (t_к - t₀)

Значение среднего ускорения в СИ измеряют в метрах на секунду в квадрате (м/с²), так как скорость измеряют в метрах в секунду, а время – в секундах.

Поясним сказанное на примерах.

Пусть автомобиль в некоторый начальный момент времени t₀ = 0 двигался в положительном направлении оси X, как показано на рис. 53, а, со скоростью, имевшей значение v₀ = 10 м/с. К моменту времени t_к = 2 с значение его скорости увеличилось до v_к = 16 м/с (автомобиль разгонялся), а направление движения осталось неизменным. Поэтому в соответствии с определением значение среднего ускорения автомобиля за эти две секунды

a_ср = (v_к - v₀) / (t_к - t₀) = (16 - 10) / (2 - 0) = 3 (м/с²).

Так как увеличение значения скорости происходило в положительном направлении оси X, то и изменение скорости, а следовательно, и значение среднего ускорения будут положительными.

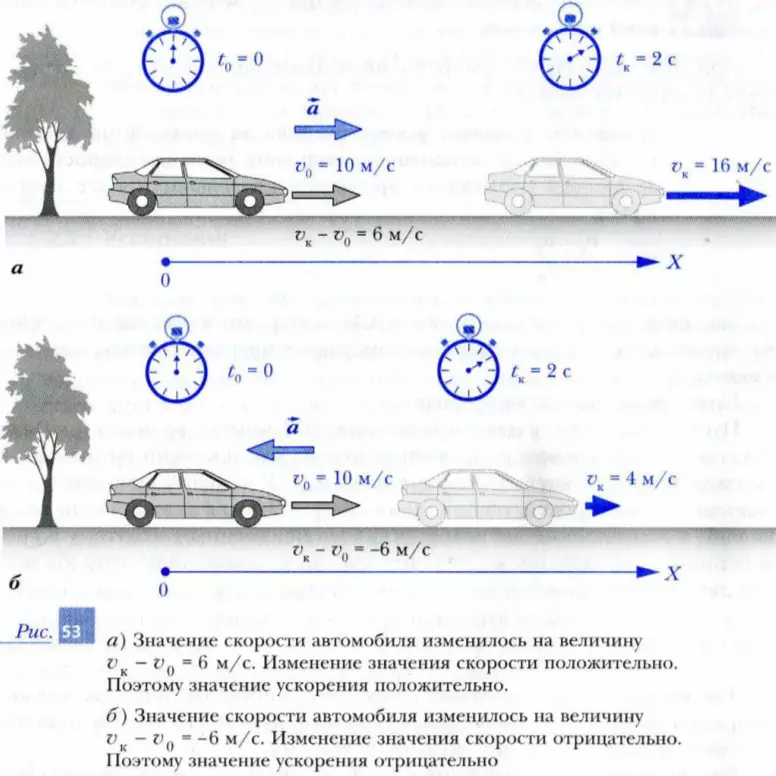
Значение среднего ускорения a = 3 м/с² означает, что за каждую секунду скорость автомобиля увеличивалось в среднем на 3 м/с.

Пусть теперь автомобиль, который в начальный момент двигался в положительном направлении оси X со скоростью, имеющей значение v₀ = 10 м/с, за две секунды уменьшил свою скорость до v_к = 4 м/с (рис. 53, б). Тогда по определению значение среднего ускорения за эти две секунды будет таким же но модулю, как и в первом случае, но противоположным но знаку:

a_ср = (v_к - v₀) / (t_к - t₀) = (4 - 10) / (2 - 0) = -3 (м/с²).

Так как значение скорости уменьшается (v_к < v₀), то и изменение значения скорости Δv, и значение среднего ускорения получаются отрицательными.

Значение среднего ускорения a = -3 м/с² означает, что за каждую секунду скорость автомобиля уменьшалась в среднем на 3 м/с (автомобиль тормозил).

Поскольку скорость является векторной величиной, то и изменение скорости – тоже вектор. Из рис. 53 следует, что, когда происходит разгон автомобиля, вектор изменения скорости направлен туда же, куда направлен вектор скорости.

Когда скорость автомобиля уменьшается (при торможении), вектор изменения скорости направлен противоположно вектору скорости.

Средним ускорением тела за промежуток времени Δt называют физическую величину, равную отношению изменения скорости этого тела за промежуток времени Δt к длительности этого промежутка.

a_ср = Δv/Δt

Из определения видно, что среднее ускорение является векторной величиной.

Направление среднего ускорения совпадает с направлением вектора изменения скорости за рассматриваемый промежуток времени.

Из определения следует, что среднее ускорение в СИ измеряют в метрах на секунду в квадрате (м/с²), так как скорость измеряют в метрах в секунду, а время – в секундах.

При уменьшении рассматриваемого промежутка времени до достаточно малого мы придем к понятию ускорения в данный момент времени.

Так же как и при определении мгновенной скорости, можно сказать, что

ускорение в данный момент времени t – это среднее ускорение за достаточно малый промежуток времени Δt, который начинается сразу после момента времени t.

Смысл словосочетания «достаточно малый промежуток времени» остается тем же самым, что и в предыдущем параграфе. Под этим промежутком подразумевается настолько малый промежуток времени, что его дальнейшее уменьшение не приводит к заметным изменениям определяемой нами величины (здесь — ускорения!).

Итоги

Величину, характеризующую быстроту изменения скорости, называют ускорением.

В СИ ускорение измеряют в метрах на секунду в квадрате (м/с²).

Значением среднего ускорения тела за промежуток времени Δt = t_к - t₀ называют отношение изменения значения скорости тела за данный промежуток времени к длительности этого промежутка.

a_ср = (v_к - v₀) / (t_к - t₀)

Вопросы

1. Что такое ускорение тела? Приведите примеры движения тела с ускорением.
2. Дайте определение значения среднего ускорения тела. Назовите единицу ускорения в СИ.
3. Какой знак имеет значение ускорения при прямолинейном движении в положительном направлении оси X, если тело: а) разгоняется; б) тормозится? Куда при этом направлен вектор ускорения?

Упражнения

1. Велосипедист, двигаясь в положительном направлении оси X, за 10 с увеличил свою скорость на 20 м/с. Определите значение среднего ускорения велосипедиста за этот промежуток времени.
2. Мотоциклист, приближаясь к повороту, уменьшает модуль своей скорости от 108 до З6 км/ч. Определите значение среднего ускорения мотоциклиста, если он тормозил в течение 5 с. Считайте, что направление движения мотоциклиста совпадает с положительным направлением координатной оси.