Перемещение. Путь

До сих пор мы рассматривали только прямолинейное равномерное движение. При этом точечные тела двигались в выбранной системе отсчета либо в положительном, либо в отрицательном направлении оси координат X. Мы установили, что в зависимости от направления движения тела, например, за промежуток времени от момента t₁ до момента t₂ изменение координаты тела (x₂ - x₁) может быть положительным, отрицательным или равным нулю (если x₂ = x₁).

Изменение координаты x₂ - x₁ принято обозначать символом Δx₁₂ (читается «дельта икс один, два»). Эта запись означает, что за промежуток времени от момента t₁ до момента t₂ изменение координаты тела Δx₁₂ = x₂ - x₁. Таким образом, если тело двигалось в положительном направлении оси X выбранной системы координат (x₂ > x₁), то Δx₁₂ > 0. Если же движение происходило в отрицательном направлении оси X (x₂1), то Δx₁₂

Результат движения удобно определять с помощью векторной величины. Такой векторной величиной является перемещение.

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец – с конечным положением точки.

Как и любую векторную величину, перемещение характеризуют модулем и направлением.

Записывать вектор перемещения точки за промежуток времени от t₁ до t₂ мы будем следующим способом: Δx₁₂.

Поясним сказанное на примере. Пусть некоторая точка A (точечное чело) движется в положительном направлении оси X и за промежуток времени от t₁ до t₂ перемещается из точки с координатой x₁ в точку с большей координатой x₂ (рис. 44). В этом случае вектор перемещения направлен в положительном направлении оси X, а его модуль равен изменению координаты за рассматриваемый промежуток времени: Δx₁₂ = x₂ - x₁ = (5 - 2) м = 3 м.

На рис. 45 изображено точечное тело В, которое движется в отрицательном направлении оси X. За промежуток времени от t₁ до t₂ оно перемещается из точки с большей координатой x₁ в точку с меньшей координатой x₂. В результате изменение координаты точки B за рассматриваемый промежуток времени Δx₁₂ = x₂ - x₁ = (2 - 5) м = -3 м. Вектор перемещения в этом случае будет направлен в отрицательном направлении оси X, а его модуль |Δx₁₂| равен 3 м. Из рассмотренных примеров можно сделать следующие выводы.

Направление перемещения при прямолинейном движении в одном направлении совпадает с направлением движения.

Модуль вектора перемещения равен модулю изменения координаты тела за рассматриваемый промежуток времени.

В повседневной жизни для описания конечного результата движения используют понятие «путь». Обычно путь обозначают символом S.

Путь – это все расстояние, пройденное точечным телом за рассматриваемый промежуток времени.

Как и любое расстояние, путь – величина неотрицательная. Например, путь, пройденный точкой A в рассмотренном примере (см. рис. 44), равен трем метрам. Путь, пройденный точкой B, также равен трем метрам.

В рассмотренных примерах (см. рис. 44 и 45) тело все время двигалось в каком-либо одном направлении. Поэтому пройденный им путь равен модулю изменения координаты тела и модулю перемещения: s12 = |Δx₁₂|.

Если тело двигалось все время в одном направлении, то пройденный им путь равен модулю перемещения и модулю изменения координаты.

Ситуация изменится, если тело в течение рассматриваемого промежутка времени изменяет направление движения.

На рис. 46 изображено, как двигалось точечное тело с момента t₀ = 0 до момента t₂ = 7 с. До момента t₁ = 4 с движение происходило равномерно в положительном направлении оси X. В результате чего изменение координаты Δx₀₁ = x₁ - x₀ = (11 - 3) м = -8 м. После этого тело стало двигаться в отрицательном направлении оси X до момента t₂ = 7 с. При этом изменение его координаты Δx₁₂ = x₂ - x₁ = (5 - 11) м = -6 м. График этого движения приведен на рис. 47.

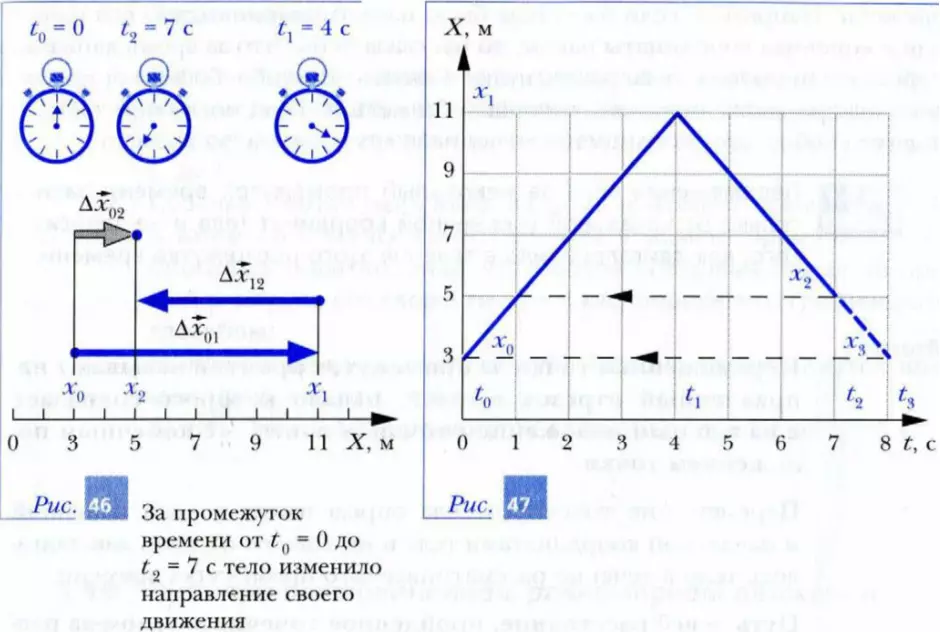
Определим изменение координаты и перемещение тела за промежуток времени от t₀ = 0 до t₂ = 7 с. В соответствии с определением изменение координаты Δx₀₂ = x₂ - x₀ = 2 м > 0. Поэтому перемещение Δx₀₂ направлено в положительном направлении оси Х, а его модуль равен 2 м.

Теперь определим путь, который прошло тело за тот же промежуток времени от t₀ = 0 до t₂ = 7 с. Сначала тело прошло 8 м в одном направлении (что соответствует модулю изменения координаты Δx₀₁), а затем 6 м в обратном направлении (эта величина соответствует модулю изменения координаты Δx₁₂). Значит, всего тело прошло 8 + 6 = 14 (м). По определению пути за промежуток времени от t₀ до t₂ тело прошло путь s₀₂ = 14 м.

Разобранный пример позволяет сделать вывод:

В случае, когда тело в течение рассматриваемого промежутка времени меняет направление своего движения, путь (все пройденное телом расстояние) больше и модуля перемещения тела, и модуля изменения координаты тела.

Теперь представьте себе, что тело после момента времени t₂ = 7 с продолжило свое движение в отрицательном направлении оси X до момента t₃ = 8 с в соответствии с законом, изображенным на рис. 47 пунктирной линией. В результате в момент времени t₃ = 8 с координата тела стала равна x₃ = 3 м. Нетрудно определить, что в этом случае перемещение тела за промежуток времени от t₀ до t₃ с равно Δx₁₃ = 0.

Ясно, что если нам известно только перемещение тела за время его движения, то мы не можем сказать как двигалось тело в течение этого времени. Например, если бы о теле было известно только, что его начальная и конечная координаты равны, то мы сказали бы, что за время движения перемещение этого тела равно нулю. Сказать что-либо более конкретное о характере движения этого тела было бы нельзя. Тело могло при таких условиях вообще стоять на месте в течение всего промежутка времени.

Перемещение тела за некоторый промежуток времени зависит только от начальной и конечной координат тела и не зависит от того, как двигалось тело в течение этого промежутка времени.

Итоги

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец – с конечным положением точки.

Перемещение точечного тела определяется только конечной и начальной координатами тела и не зависит от того, как двигалось тело в течение рассматриваемого промежутка времени.

Путь – все расстояние, пройденное точечным телом за рассматриваемый промежуток времени.

Если тело в процессе движения не меняло направления движения, то пройденный этим телом путь равен модулю его перемещения.

Если тело в течение рассматриваемого промежутка времени меняло направление своего движения, путь больше и молуля перемещения тела, и модуля изменения координаты тела.

Путь всегда величина неотрицательная. Он равен нулю только в том случае, если в течение всего рассматриваемого промежутка времени тело покоилось (стояло на месте).

Вопросы

1. Что такое перемещение? От чего оно зависит?
2. Что такое путь? От чего он зависит?
3. Чем путь отличается от перемещения и изменения координаты за один и тот же промежуток времени, в течение которого тело двигалось прямолинейно, не изменяя направления движения?

Упражнения

1. Используя закон движения в графической форме, представленный на рис. 47, опишите характер движения тела (направление, скорость) в разные промежутки времени: от t₀ до t₁, от t₁ до t₂, от t₂ до t₃.
2. Собачка Протон выбежала из дома в момент времени t₀ = 0, а затем по команде своего хозяина в момент времени t₄ = 4 с бросилась обратно. Зная, что Протон все время бежал по прямой и модуль его скорости |v| = 4 м/с, определите графическим способом: а) изменение координаты и путь Протона за промежуток времени от t₀ = 0 до t₆ = 6 с; б) путь Протона за промежуток времени от t₂ = 2 с до t₅ = 5 с.